
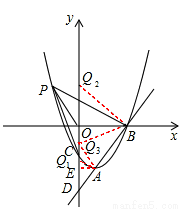
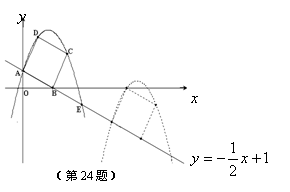
如图,已知直线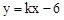 与抛物线
与抛物线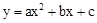 相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
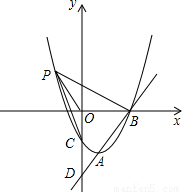
(1)求抛物线的解析式;
(2)在(1)中抛物线的第二象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标。
解:(1)把A(1,-4)代入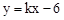 ,得k=2,∴
,得k=2,∴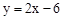 。
。
令y=0,解得:x=3,∴B的坐标是(3,0)。
∵A为顶点,∴设抛物线的解析为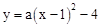 。
。
把B(3,0)代入得:4a-4=0,解得a=1。
∴抛物线的解析式为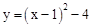 即
即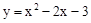 。
。
(2)存在。
∵OB=OC=3,OP=OP,∴当∠POB=∠POC时,△POB≌△POC。
此时PO平分第二象限,即PO的解析式为y=-x。
设P(m,-m),则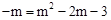 ,解得
,解得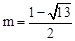 (
(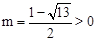 ,舍去)。
,舍去)。
∴P(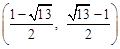 。
。
(3)①如图,当∠Q1AB=90°时,△DAQ1∽△DOB,
∴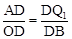 ,即
,即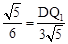 。∴
。∴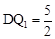 。
。
∴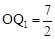 ,即
,即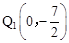 。
。
②如图,当∠Q2BA=90°时,△BOQ2∽△DOB,
∴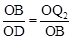 ,即
,即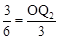 。
。
∴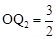 ,即
,即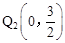 。
。
③如图,当∠AQ3B=90°时,作AE⊥y轴于E,则△BOQ3∽△Q3EA,
∴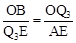 ,即
,即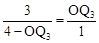 。
。
∴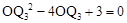 ,解得OQ3=1或3,即Q3(0,-1),Q4(0,-3)。
,解得OQ3=1或3,即Q3(0,-1),Q4(0,-3)。
综上,Q点坐标为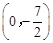 或
或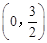 或(0,-1)或(0,-3)。
或(0,-1)或(0,-3)。
【解析】
试题分析:(1)已知点A坐标可确定直线AB的解析式,进一步能求出点B的坐标.点A是抛物线的顶点,那么可以将抛物线的解析式设为顶点式,再代入点B的坐标,依据待定系数法可解。
(2)首先由抛物线的解析式求出点C的坐标,在△POB和△POC中,已知的条件是公共边OP,若OB与OC不相等,那么这两个三角形不能构成全等三角形;若OB等于OC,那么还要满足的条件为:∠POC=∠POB,各自去掉一个直角后容易发现,点P正好在第二象限的角平分线上,联立直线y=-x与抛物线的解析式,直接求交点坐标即可,同时还要注意点P在第二象限的限定条件。
(3)分别以A、B、Q为直角顶点,分类进行讨论,找出相关的相似三角形,依据对应线段成比例进行求解即可。


科目:初中数学 来源: 题型:
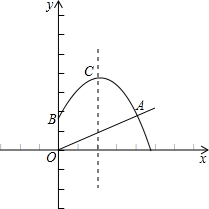 点C的坐标为(2,3.5).
点C的坐标为(2,3.5). 查看答案和解析>>
科目:初中数学 来源:中考必备’04全国中考试题集锦·数学 题型:044
如图,已知抛物y=x2-ax+a+2与x轴交于A、B两点,与y轴交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C.动点P以每秒2个单位长度的速度从点C出发,沿C→D运动.同时、点Q以每秒1个单位长度的速度从点A出发,沿A→B运动.连结PQ、CB.设点P的运动时间为t秒.

(1)求a的值;
(2)当t为何值时,PQ平行于y轴;
(3)当四边形PQBC的面积等于14时,求t的值.
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(福建龙岩卷)数学(解析版) 题型:解答题
在平面直角坐标系xoy中, 一块含60°角的三角板作如图摆放,斜边 AB在x轴上,直角顶点C在y轴正半轴上,已知点A(-1,0).
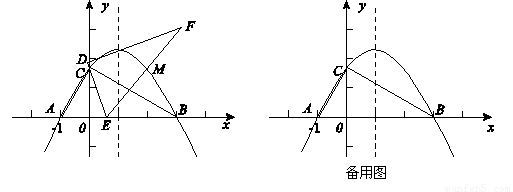
(1)请直接写出点B、C的坐标:B( , )、C( , );并求经过A、B、C三点的抛物
线解析式;
(2)现有与上述三角板完全一样的三角板DEF(其中∠EDF=90°,∠DEF=60°),把顶点E放在线段
AB上(点E是不与A、B两点重合的动点),并使ED所在直线经过点C. 此时,EF所在直线与(1)中的抛物线交于第一象限的点M.
①设AE=x,当x为何值时,△OCE∽△OBC;
②在①的条件下探究:抛物线的对称轴上是否存在点P使△PEM是等腰三角形,若存在,请求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年广西省贵港市九年级第一次教学质量监测数学卷 题型:解答题
(本题满分12分)
如图所示,在平面直角坐标系中,顶点为(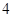 ,
,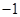 )的抛物线交
)的抛物线交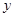 轴于
轴于 点,交
点,交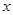 轴于
轴于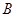 ,
,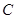 两点(点
两点(点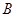 在点
在点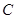 的左侧),
已知
的左侧),
已知 点坐标为(
点坐标为( ,
,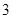 ).
).
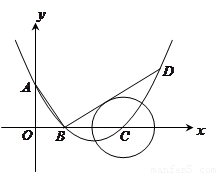
(1)求此抛物线的解析式;
(2)过点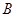 作线段
作线段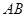 的垂线交抛物线于点
的垂线交抛物线于点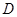 ,
,
如果以点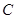 为圆心的圆与直线
为圆心的圆与直线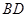 相切,请判断抛物
相切,请判断抛物
线的对称轴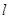 与⊙
与⊙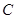 有怎样的位置关系,并给出证明;
有怎样的位置关系,并给出证明;
(3)已知点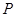 是抛物线上的一个动点,且位于
是抛物线上的一个动点,且位于 ,
,
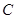 两点之间,问:当点
两点之间,问:当点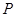 运动到什么位置时,
运动到什么位置时,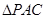 的
的
面积最大?并求出此时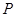 点的坐标和
点的坐标和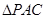 的最大面积.
的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
.如图,已 知直线 ![]() 交坐标轴于
交坐标轴于![]() 两点,以线段
两点,以线段![]()
![]() 为边向上作正方形
为边向上作正方形![]() ,过点
,过点![]() 的抛物线与直线另一个交点为
的抛物线与直线另一个交点为![]() .
.
(1)请直接写出点![]() 的坐标;
的坐标;
(2)求抛物线的解析式;
(3)若正方形以每秒![]() 个单位长度的速度沿射线
个单位长度的速度沿射线![]() 下滑,直至顶点
下滑,直至顶点![]() 落在x轴上时停止.设正方形落在
落在x轴上时停止.设正方形落在![]() 轴下方部分的面积为
轴下方部分的面积为![]() ,求
,求![]() 关于滑行时间
关于滑行时间![]() 的函数关系式,并写出相应自变量
的函数关系式,并写出相应自变量![]() 的取值范围;
的取值范围;
(4)在(3)的条件下,抛物线与正方形一起平移,同时停止,求抛物线上![]() 两点间的抛物
两点间的抛物
线弧所扫过的面积.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com