
 的图象上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形一定有两个,如图所示,并且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.
的图象上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形一定有两个,如图所示,并且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.
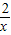 的图象上,即可求得点M的值;
的图象上,即可求得点M的值;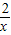 的图象上,
的图象上,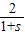 ,
,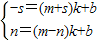 ,
,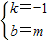 ,
,

科目:初中数学 来源: 题型:阅读理解
 25、请阅读下列材料:
25、请阅读下列材料:查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解


查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
 (2012•贵阳模拟)阅读下列材料:
(2012•贵阳模拟)阅读下列材料:| 2 | x |
查看答案和解析>>
科目:初中数学 来源:数学教研室 题型:022

综上所述,数轴上A、B两点之间的距离表示为|AB|=|a-b|.
回答下列问题:
(1)数轴上表示2和5的两点之间的距离是________,数轴上表示-2和-5的两点之间的距离是________,数轴上表示-2和5的两点之间的距离是__________;
(2)数轴上表示x和-1的两点A、B之间的距离是__________,如果|AB|=2,则x为_________;
(3)当代数式|x+1|+|x-2|取最小值时,相应的x有的取值范围是___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com