
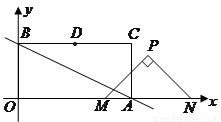
如图,直线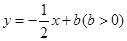 分别交
分别交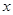 轴,
轴,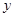 轴于
轴于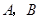 两点,以
两点,以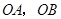 为边作矩形
为边作矩形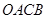 ,
,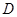 为
为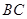 的中点.以
的中点.以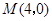 ,
,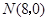 为斜边端点作等腰直角三角形
为斜边端点作等腰直角三角形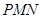 ,点
,点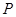 在第一象限,设矩形
在第一象限,设矩形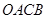 与
与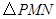 重叠部分的面积为
重叠部分的面积为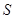 .
.
(1)求点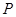 的坐标;
的坐标;
(2)当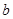 值由小到大变化时,求
值由小到大变化时,求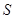 与
与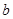 的函数关系式;
的函数关系式;
(3)若在直线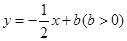 上存在点
上存在点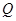 ,使
,使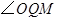 等于
等于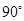 ,求出
,求出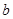 的取值范围;
的取值范围;
(4)在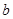 值的变化过程中,若
值的变化过程中,若 为等腰三角形,请直接写出所有符合条件的
为等腰三角形,请直接写出所有符合条件的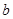 值.
值.
解: (1)作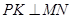 于
于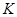 ,则
,则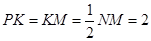 .
.
 ,
,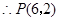 .
.
(2)当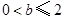 时,如图①,
时,如图①,

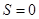 .
.
当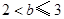 时,如图②,
时,如图②,
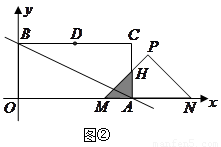
设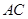 交
交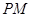 于
于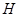 .
.
 .
.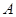
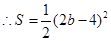 .
.
即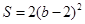 .
.
或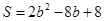 .
.
当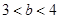 时,如图③,
时,如图③,
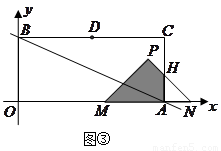
设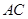 交
交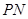 于
于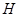 .
.
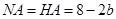 .
.
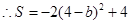 ,
,
或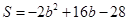 .
.
当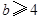 时,如图④,
时,如图④,
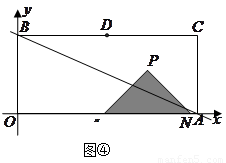
 .
.
(此问不画图不扣分)
(3) .
.
(提示:以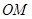 为直径作圆,当直线
为直径作圆,当直线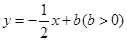
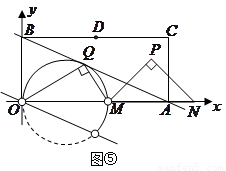
与此圆相切时,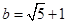 .)
.)
(4)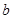 的值为
的值为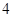 ,
,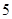 ,
,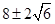 .
.
(提示:当 时,
时,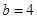 .
.
当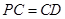 时,
时,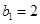 (舍),
(舍), .
.
当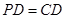 时,
时,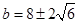 .)
.)
【解析】(1)作出作PK⊥MN于K,利用等腰三角形的性质得出KO的长,即可出P点的坐标;
(2)利用关于x轴对称的性质得出P′点的坐标,再利用交点式求出二次函数解析式即可;
(3)分别利用当0<b≤2时,当2<b≤3时以及当3<b<4时和当b≥4时结合图象求出即可;
(4)分PC为腰或底两种情况分析。


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
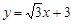 分别交
分别交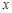 轴、
轴、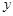 轴于B、A两点,抛物线L:
轴于B、A两点,抛物线L: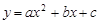 的顶点G在
的顶点G在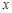 轴上,且过(0,4)和(4,4)两点.
轴上,且过(0,4)和(4,4)两点.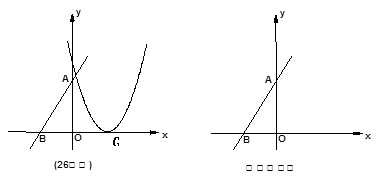
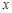 轴平行移动得抛物线L
轴平行移动得抛物线L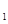 ,其顶点为P,同时将△PAB沿直线AB翻折得到△DAB,使点D落在抛物线L
,其顶点为P,同时将△PAB沿直线AB翻折得到△DAB,使点D落在抛物线L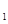 上. 试问这样的抛物线L
上. 试问这样的抛物线L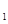 是否存在,若存在,求出L
是否存在,若存在,求出L 对应的函数关系式,若不存在,说明理由.
对应的函数关系式,若不存在,说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
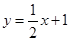 分别交
分别交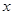 轴,
轴,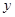 轴于点
轴于点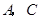 ,点
,点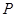 是直线
是直线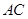 与双曲线
与双曲线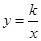 在第一象限内的交点,
在第一象限内的交点,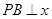 轴,垂足为点
轴,垂足为点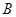 ,
,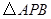 的面积为4.
的面积为4.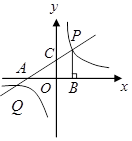
 的坐标;
的坐标; 的坐标.
的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:
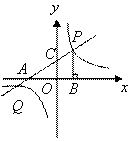
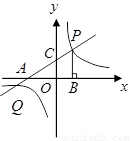
如图,直线![]() 分别交
分别交![]() 轴,
轴,![]() 轴于点
轴于点![]() ,点
,点![]() 是直线
是直线![]() 与双曲线
与双曲线![]() 在第一象限内的交点,
在第一象限内的交点,![]() 轴,垂足为点
轴,垂足为点![]() ,
,![]() 的面积为4.
的面积为4.
(1)求点![]() 的坐标;
的坐标;
(2)求双曲线的解析式及直线与双曲线另一交点![]() 的坐标.
的坐标.
 |
查看答案和解析>>
科目:初中数学 来源:2012届广东省汕头市潮南区中考模拟考试数学卷(带解析) 题型:解答题
如图,直线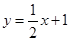 分别交
分别交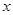 轴,
轴,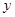 轴于点
轴于点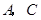 ,点
,点 是直线
是直线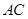 与双曲线
与双曲线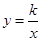 在第一象限内的交点,
在第一象限内的交点,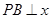 轴,垂足为点
轴,垂足为点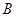 ,
,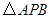 的面积为4.
的面积为4.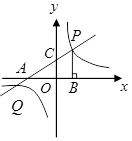
(1)求点 的坐标;
的坐标;
(2)求双曲线的解析式及直线与双曲线另一交点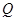 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年广东省汕头市潮南区中考模拟考试数学卷(解析版) 题型:解答题
如图,直线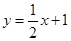 分别交
分别交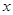 轴,
轴,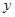 轴于点
轴于点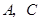 ,点
,点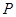 是直线
是直线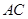 与双曲线
与双曲线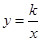 在第一象限内的交点,
在第一象限内的交点,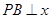 轴,垂足为点
轴,垂足为点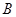 ,
,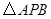 的面积为4.
的面积为4.
(1)求点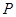 的坐标;
的坐标;
(2)求双曲线的解析式及直线与双曲线另一交点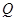 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com