
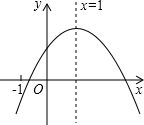
 二次函数的图象如图所示,对称轴为x=1,给出下列结论:①abc<0;②b2>4ac;③4a+2b+c<0;④2a+b=0.其中正确的结论有( )
二次函数的图象如图所示,对称轴为x=1,给出下列结论:①abc<0;②b2>4ac;③4a+2b+c<0;④2a+b=0.其中正确的结论有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 根据图象得出a>0,-$\frac{b}{2a}$=1,c>0,结合图象上的点和对称轴即可逐项判断.
解答 解:①∵二次函数的图象的开口向下,
∴a<0,
∵二次函数的图象y轴的交点在y轴的正半轴上,
∴c>0,
∵二次函数图象的对称轴是直线x=1,
∴-$\frac{b}{2a}$=1,
∴2a+b=0,b>0
∴abc<0,故正确;
②∵抛物线与x轴有两个交点,
∴b2-4ac>0,
∴b2>4ac,
故正确;
③∵二次函数图象的对称轴是直线x=1,
∴抛物线上x=0时的点与当x=2时的点对称,
即当x=2时,y>0
∴4a+2b+c>0,
故错误;
④∵二次函数图象的对称轴是直线x=1,
∴-$\frac{b}{2a}$=1,
∴2a+b=0,
故正确.
综上所述,正确的结论有3个.
故选:B.
点评 本题考查了二次函数的图象与系数的关系的应用,题目比较典型,主要考查学生的理解能力和辨析能力.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(6,9).双曲线y=$\frac{k}{x}$(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(6,9).双曲线y=$\frac{k}{x}$(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
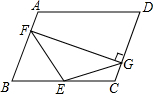 如图,?ABCD中,∠B=70°,点E是BC的中点,且BF=BE,过点F作FG⊥CD于点G,有如下结论:①EF=EG;②∠EFG=35°;③CE=DG;④∠FEG=100°;⑤∠EGC=55°,则正确的结论是①②⑤.(填序号即可)
如图,?ABCD中,∠B=70°,点E是BC的中点,且BF=BE,过点F作FG⊥CD于点G,有如下结论:①EF=EG;②∠EFG=35°;③CE=DG;④∠FEG=100°;⑤∠EGC=55°,则正确的结论是①②⑤.(填序号即可)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com