Question

7．一个长为10、宽为2的矩形纸条ABCD，沿图（1）所示方式折叠，∠DEF=30°，折痕为EF，ED′与BC交于点G，得到图（2），在图（2）中，过点G作GM⊥EF，点M为垂足，将纸条沿GM再次折叠，折痕GM两旁的部分能完全重合，如图（3），则AE的长为5-$\sqrt{3}$．

Answer 1

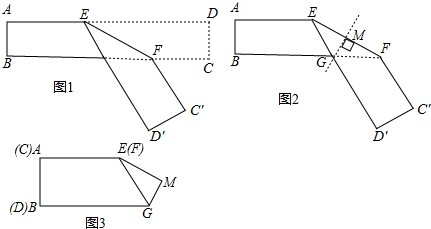
分析 如图1中，延长CF交AD于H，连接HG交EF于M，作EK⊥BC于K，先证明四边形EGFH是菱形，四边形ABKE是矩形，设AE=x，根据AE+EG+BK+KG=10列出方程即可解决．

解答 解：如图1中，延长CF交AD于H，连接HG交EF于M，作EK⊥BC于K．

∵EH∥GF，EG∥HF，
∴四边形EGHF是平行四边形，
∵∠DEF=∠EFB=∠FEG=30°，
∴GE=FG，
∴四边形EGFH是菱形，∠HEG=60°，
∴EH=EG=GF=FH，
∴△EGH，△HGF都是等边三角形．设AE=x，
∵∠A=∠B=∠EKB=90°，
∴四边形ABKE是矩形，
∴AE=BK=x，AB=EK=2，
在RT△EKG中，∵∠KEG=30°，EK=2，
∴KG=$\frac{2\sqrt{3}}{3}$，EG=$\frac{4\sqrt{3}}{3}$，
∵AE+DE=AE+ED′=AE+EG+BG=AE+EG+BK+KG=10，
∴x+$\frac{4\sqrt{3}}{3}$+x+$\frac{2\sqrt{3}}{3}$=10，
x=5-$\sqrt{3}$．
故答案为5-$\sqrt{3}$．

点评 本题考查翻折变换、矩形的判定和性质、菱形的判定和性质、直角三角形中30度角的性质，解题的关键是用方程的思想去思考，属于中考常考题型．