
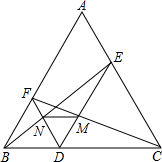
 如图,点D是等边△ABC中BC边上一点,过点D分别作DE∥AB,DF∥AC,交AC,AB于E,F,连接BE,CF,分别交DF,DE于点N,M,连接MN.试判断△DMN的形状,并说明理由.
如图,点D是等边△ABC中BC边上一点,过点D分别作DE∥AB,DF∥AC,交AC,AB于E,F,连接BE,CF,分别交DF,DE于点N,M,连接MN.试判断△DMN的形状,并说明理由. 分析 根据平行线分线段成比例定理,得到$\frac{CM}{MF}$=$\frac{NE}{BN}$,证明MN∥BC,证明结论.
解答 解:△DMN为等边三角形,
∵DE∥AB,且△ABC为等边三角形
∴∠EDC=∠ABC=60°,
$\frac{CM}{MF}$=$\frac{CD}{BD}$,$\frac{BN}{NE}$=$\frac{BD}{CD}$,
∴$\frac{CM}{MF}$=$\frac{NE}{BN}$,
∴MN∥BC,
∴∠MND=∠BDN=60°,∠MND=∠MDC=60°,
∴△DMN为等边三角形.
点评 本题考查的是平行线分线段成比例,掌握平行线分线段成比例定理和等边三角形的判定和性质是解题的关键.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 33.8×104 | B. | 3.38×104 | C. | 3.38×105 | D. | 0.338×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,直线y1=x+b与双曲线y2=$\frac{k}{x}$交于点A(1,4)和点B,经过点A的另一条直线与双曲线y2=$\frac{k}{x}$交于点C.则:
如图,直线y1=x+b与双曲线y2=$\frac{k}{x}$交于点A(1,4)和点B,经过点A的另一条直线与双曲线y2=$\frac{k}{x}$交于点C.则:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
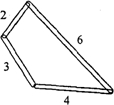 如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依次为2、3、4、6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任意两个螺丝间的距离的最大值为( )
如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依次为2、3、4、6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任意两个螺丝间的距离的最大值为( )| A. | 6 | B. | 7 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一线段AB=10米,P点从A点出发匀速沿AB方向运动到终点B需2.5分钟,Q点从B点出发匀速沿BA方向运动到终点A需2分钟.现P、Q两点同时出发相向而行,在任一点到达终点后,两点即同时停止运动.设运动时间为x分钟.P、Q两点间的距离为y米,y与x的函数关系如图.
一线段AB=10米,P点从A点出发匀速沿AB方向运动到终点B需2.5分钟,Q点从B点出发匀速沿BA方向运动到终点A需2分钟.现P、Q两点同时出发相向而行,在任一点到达终点后,两点即同时停止运动.设运动时间为x分钟.P、Q两点间的距离为y米,y与x的函数关系如图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com