
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
①当x>3时,y<0;②3a+b<0;③﹣1≤a≤﹣ ![]() ;④4ac﹣b2>8a;
;④4ac﹣b2>8a;
其中正确的结论是( )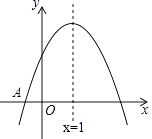
A.①③④
B.①②③
C.①②④
D.①②③④
【答案】B
【解析】解:①由抛物线的对称性可求得抛物线与x轴令一个交点的坐标为(3,0),当x>3时,y<0,故①正确;
②抛物线开口向下,故a<0,
∵x=﹣ ![]() =1,
=1,
∴2a+b=0.
∴3a+b=0+a=a<0,故②正确;
③设抛物线的解析式为y=a(x+1)(x﹣3),则y=ax2﹣2ax﹣3a,
令x=0得:y=﹣3a.
∵抛物线与y轴的交点B在(0,2)和(0,3)之间,
∴2≤﹣3a≤3.
解得:﹣1≤a≤﹣ ![]() ,故③正确;
,故③正确;
④.∵抛物线y轴的交点B在(0,2)和(0,3)之间,
∴2≤c≤3,
由4ac﹣b2>8a得:4ac﹣8a>b2 ,
∵a<0,
∴c﹣2< ![]()
∴c﹣2<0
∴c<2,与2≤c≤3矛盾,故④错误.
故选:B.
①先由抛物线的对称性求得抛物线与x轴令一个交点的坐标为(3,0),从而可知当x>3时,y<0;
②由抛物线开口向下可知a<0,然后根据x=﹣ ![]() =1,可知:2a+b=0,从而可知3a+b=0+a=a<0;
=1,可知:2a+b=0,从而可知3a+b=0+a=a<0;
③设抛物线的解析式为y=a(x+1)(x﹣3),则y=ax2﹣2ax﹣3a,令x=0得:y=﹣3a.由抛物线与y轴的交点B在(0,2)和(0,3)之间,可知2≤﹣3a≤3.④由4ac﹣b2>8a得c﹣2<0与题意不符.


科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,EG、EM、FM分别平分∠AEF,∠BEF,∠EFD,则图中与∠DFM相等的角(不含它本身)的个数为( )

A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如图两幅统计图(不完整).
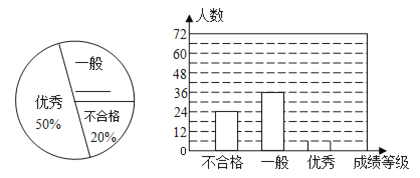
请你根据图中所给的信息解答下列问题:
(1)这次测试,一共抽取了名学生;
(2)请将以上两幅统计图补充完整;(注:扇形图补百分比,条形图补“优秀”人数与高度);
(3)若“一般”和“优秀”均被视为达标成绩,该校学生有1200人,请你估计此次测试中,全校达标的学生有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠C=90°,AB的垂直平分线MN交BC于点D.
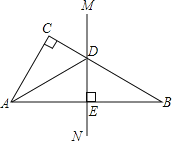
(1)如果∠CAD=20°,求∠B的度数;
(2)如果∠CAB=50°,求∠CAD的度数;
(3)如果∠CAD:∠DAB=1:2,求∠CAB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级全体学生在5名教师的带领下去公园秋游,公园的门票为每人30元.现有两种优惠方案,甲方案:带队老师免费,学生按8折收费;乙方案:师生都按7.5折收费.
(1)若有n名学生,用含n的代数式表示两种优惠方案各需多少元?
(2)当n=70时,采用哪种方案更优惠?
(3)当n=100时,采用哪种方案更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x、y的方程组![]() (实数m是常数).
(实数m是常数).
(1)若x+y=1,求实数m的值;
(2)若-1≤x-y≤5,求m的取值范围;
(3)在(2)的条件下,化简:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用长度相等的小棒按一定规律摆成的一组图案.
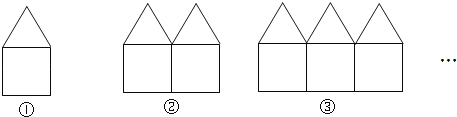
(1)第1个图案中有______根小棒;第2个图案中有__根小棒;第3个图案中有__根小棒;
(2)第n个图案中有多少根小棒?
(3)第25个图案中有多少根小棒?
(4)是否存在某个符合上述规律的图案,由2032根小棒摆成?如果有,指出是第几个图案;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人想共同承包一项工程,甲单独做30天完成,乙单独做20天完成,合同规定15天完成,若完不成视为违约,甲乙两人经过商量后签订了该合同.
(1)正常情况下,甲乙两人能否履行该合同?为什么?
(2)现在两人合作了9天,因别处有急事,必需调走1人,问两人能否违约?
查看答案和解析>>
科目:初中数学 来源: 题型:
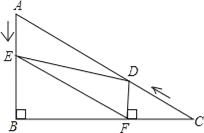
【题目】如图,在Rt△ABC中,∠B=90°,BC=5![]() ,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
(1)AC的长是 ,AB的长是 .
(2)在D、E的运动过程中,线段EF与AD的关系是否发生变化?若不变化,那么线段EF与AD是何关系,并给予证明;若变化,请说明理由.
(3)当t为何值,△BEF的面积是2![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com