
分析 (1)根据题意列出函数关系式即可得到结论;
(2)根据题意,令利润等于8000,然后再根据y关于x的关系式,从而可以解答本题.
解答 解:(1)根据题意得:y=(x-3)[500-10(x-40)]=-10x2+1200x-27000,
配方得,y=-10(x-60)2+9000,
∵a<0,
∴x<60时,y随x的增大而减小,
∵该品牌粽子售价不能超过进价的180%,
∴当x=54时,y由最大值,此时,y=-10×(54-60)2+9000=8640,
∴当售价为每盒54元时,获得的最大利润是8640元;
(2)令y=8000,-10x2+1200x-27000=8000,
解得:x1=50,x2=70,
∴50≤x≤70时,y≥8000,
∵x≤54,
∴50≤x≤54时,y≥8000,
即超市想要每天获得利润不少于8000元,售价的范围是50≤x≤54.
点评 本题考查二次函数的应用,一元二次方程的应用,解题的关键是明确题意,找出所求问题需要的条件.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10(1+x)2=16.9 | B. | 10(1+2x)=16.9 | C. | 10(1-x)2=16.9 | D. | 10(1-2x)=16.9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+y=50}\\{\frac{2}{3}x+y=50}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+2y=50}\\{\frac{2}{3}x+y=50}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{\frac{1}{2}x+y=50}\\{x+\frac{2}{3}y=50}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+\frac{1}{2}y=50}\\{\frac{2}{3}x+y=50}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
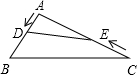 如图,在钝角△ABC中,AB=5cm,AC=10cm,动点D从A点出发到B点止,动点E从C点出发到A点止,点D运动的速度为1cm/秒,点E运动的速度为2cm/秒,如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是( )
如图,在钝角△ABC中,AB=5cm,AC=10cm,动点D从A点出发到B点止,动点E从C点出发到A点止,点D运动的速度为1cm/秒,点E运动的速度为2cm/秒,如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是( )| A. | 2.5秒 | B. | 4.5秒 | C. | 2.5秒或4.5秒 | D. | 2.5秒或4秒 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
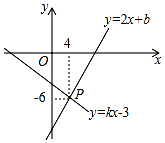 如图,已知一次函数y=2x+b和y=kx-3(k≠0)的图象交于点P,则二元一次方程组$\left\{\begin{array}{l}2x-y=-b\\ kx-y=3\end{array}\right.$的解是$\left\{\begin{array}{l}{x=4}\\{y=-6}\end{array}\right.$.
如图,已知一次函数y=2x+b和y=kx-3(k≠0)的图象交于点P,则二元一次方程组$\left\{\begin{array}{l}2x-y=-b\\ kx-y=3\end{array}\right.$的解是$\left\{\begin{array}{l}{x=4}\\{y=-6}\end{array}\right.$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com