
 如图所示,C在BD上,且BC=3,CD=2,△ABC,△ECD均为等边三角形,AD与CE交于F,则△ACF的周长:△EDF的周长的值为
如图所示,C在BD上,且BC=3,CD=2,△ABC,△ECD均为等边三角形,AD与CE交于F,则△ACF的周长:△EDF的周长的值为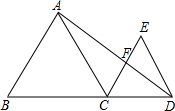 ∵△ABC,△ECD均为等边三角形,
∵△ABC,△ECD均为等边三角形,

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
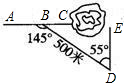 如图所示,施工队在沿AC方向开山修路,为了加快施工进度,要在小山的另一边点E同时施工,从AC上的一点B,取∠ABD=145°,BD=500米,∠D=55°,要使A,C,E成一直线,那么开挖点E离点B的距离如何求得?请你设计出解决方案.
如图所示,施工队在沿AC方向开山修路,为了加快施工进度,要在小山的另一边点E同时施工,从AC上的一点B,取∠ABD=145°,BD=500米,∠D=55°,要使A,C,E成一直线,那么开挖点E离点B的距离如何求得?请你设计出解决方案.查看答案和解析>>
科目:初中数学 来源:黄冈难点课课练八年级数学下册(北师大版) 题型:022
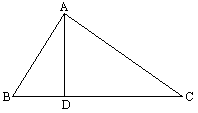
已知:如图所示,D在BC上,△ABD∽△CAD,BD=4,CD=9,则△ABD与△CAD的相似比为________.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年九年级(上)优秀生调研考试数学试卷(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com