
 26、如图,已知点从M,N分别在等边△ABC的边BC、CA上,AM,BN交于点Q,且∠BQM=60°.求证:BM=CN.
26、如图,已知点从M,N分别在等边△ABC的边BC、CA上,AM,BN交于点Q,且∠BQM=60°.求证:BM=CN.科目:初中数学 来源:2008年初中毕业升学考试(江苏无锡卷)数学(带解析) 题型:解答题
如图,已知点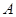 从
从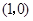 出发,以1个单位长度/秒的速度沿
出发,以1个单位长度/秒的速度沿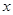 轴向正方向运动,以
轴向正方向运动,以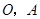 为顶点作菱形
为顶点作菱形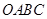 ,使点
,使点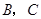 在第一象限内,且
在第一象限内,且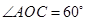 ;以
;以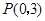 为圆心,
为圆心,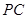 为半径作圆.设点
为半径作圆.设点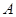 运动了
运动了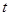 秒,求:
秒,求:
(1)点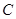 的坐标(用含
的坐标(用含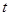 的代数式表示);
的代数式表示);
(2)当点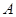 在运动过程中,所有使
在运动过程中,所有使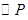 与菱形
与菱形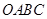 的边所在直线相切的
的边所在直线相切的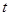 的值.
的值.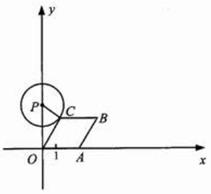
查看答案和解析>>
科目:初中数学 来源:2008年初中毕业升学考试(江苏无锡卷)数学(解析版) 题型:解答题
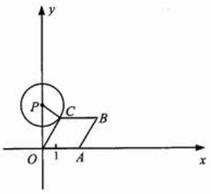
如图,已知点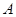 从
从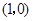 出发,以1个单位长度/秒的速度沿
出发,以1个单位长度/秒的速度沿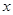 轴向正方向运动,以
轴向正方向运动,以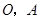 为顶点作菱形
为顶点作菱形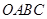 ,使点
,使点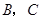 在第一象限内,且
在第一象限内,且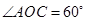 ;以
;以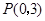 为圆心,
为圆心, 为半径作圆.设点
为半径作圆.设点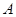 运动了
运动了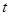 秒,求:
秒,求:
(1)点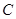 的坐标(用含
的坐标(用含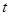 的代数式表示);
的代数式表示);
(2)当点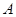 在运动过程中,所有使
在运动过程中,所有使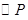 与菱形
与菱形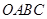 的边所在直线相切的
的边所在直线相切的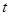 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
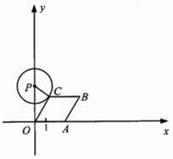
如图,已知点![]() 从
从![]() 出发,以1个单位长度/秒的速度沿
出发,以1个单位长度/秒的速度沿![]() 轴向正方向运动,以
轴向正方向运动,以![]() 为顶点作菱形
为顶点作菱形![]() ,使点
,使点![]() 在第一象限内,且
在第一象限内,且![]() ;以
;以![]() 为圆心,
为圆心,![]() 为半径作圆.设点
为半径作圆.设点![]() 运动了
运动了![]() 秒,求:
秒,求:
(1)点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 在运动过程中,所有使⊙
在运动过程中,所有使⊙![]() 与菱形
与菱形![]() 的边所在直线相切的
的边所在直线相切的![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com