
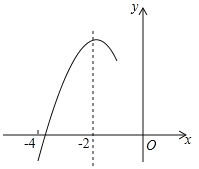
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣2,与x轴的一个交点在(﹣3,0)和(﹣4,0)之间,其部分图象如图所示,则下列结论:①4a﹣b=0;②c<0;③﹣3a+c>0;④4a﹣2b>at2+bt(t为实数);⑤点(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,
,![]() )是该抛物线上的点,则
)是该抛物线上的点,则![]() ,正确的个数有( )
,正确的个数有( )
A. 4个 B. 3个 C. 2个 D. 1个
【答案】B
【解析】解:∵抛物线的对称轴为直线x=![]() =﹣2,∴4a﹣b=0,所以①正确;
=﹣2,∴4a﹣b=0,所以①正确;
∵与x轴的一个交点在(﹣3,0)和(﹣4,0)之间,∴由抛物线的对称性知,另一个交点在(﹣1,0)和(0,0)之间,∴抛物线与y轴的交点在y轴的负半轴,即c<0,故②正确;
∵由②知,x=﹣1时y>0,且b=4a,即a﹣b+c=a﹣4a+c=﹣3a+c>0,所以③正确;
由函数图象知当x=﹣2时,函数取得最大值,∴4a﹣2b+c≥at2+bt+c,即4a﹣2b≥at2+bt(t为实数),故④错误;
∵抛物线的开口向下,且对称轴为直线x=﹣2,∴抛物线上离对称轴水平距离越小,函数值越大,∴y1<y3<y2,故⑤错误;
故选B.


科目:初中数学 来源: 题型:
【题目】如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,-1),与x轴以及y=x+1的图象分别交于点C、D,且点D的坐标为(1,n),
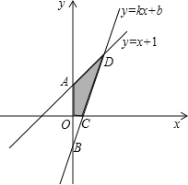
(1)求n,k ,b的值;
(2)若函数y=kx+b的函数值大于函数y=x+1的函数值,则x的取值范围是多少?
(3)求四边形AOCD的面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进了甲、乙两种型号的中性笔共4000支,甲型号中性笔进价是3元/支,乙型号中性笔进价是7元/支,购进两种型号的中性笔共用去16000元.
(1)求甲、乙两种型号的中性笔各购进了多少支;
(2)为使每支乙型号中性笔的利润是甲型号的1.8倍,且保证售完这4000支中性笔的利润不低于7200元,求每支甲型号中性笔的售价至少是多少元.(注:利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
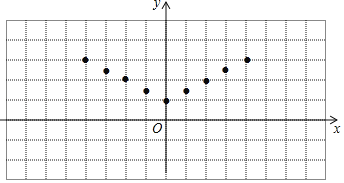
【题目】某校数学兴趣小组根据学习函数的经验,对函数y=![]() |x|+1的图象和性质进行了探究,探究过程如下:(1)自变量x的取值范围是全体实数,x与y的几组对应值如表:
|x|+1的图象和性质进行了探究,探究过程如下:(1)自变量x的取值范围是全体实数,x与y的几组对应值如表:
X | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
Y | … | 3 | 2.5 | m | 1.5 | 1 | 1.5 | 2 | 2.5 | 3 | … |
(1)其中m= .
(2)如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(3)当2<y≤3时,x的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平整的地面上,有若干个完全相同的棱长为![]() 的小正方体堆成一个几何体,如下图所示.
的小正方体堆成一个几何体,如下图所示.
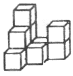



(1)该几何体是由 个小正方体组成,请画出它的主视图、左视图、俯视图(网格中所画的图形要画出各个正方形边框并涂上阴影).
(2)如果在这个几何体露在外面的表面喷上黄色的漆,每平方厘米用2克,则共需 克漆.
(3)这个几何体上,再添加一些相同的小正方体并保持这个几何体的俯视图和左视图不变,那么最多可以再添加 个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:

(Ⅰ)图1中a的值为 ;
(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数;
(Ⅲ)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m的运动员能否进入复赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
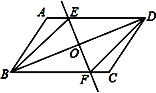
【题目】已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
(1)求证:△DOE≌△BOF.
(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为12,E是BC中点,将正方形边CD沿DE折叠到DF,将AD折叠,使AD与DF重合,折痕交AB于G,连接BF,CF,则下列结论:①G、F、E三点共线;②BG=8;③△BEF∽△CDF;④S△BFG=![]() .其中正确的有( )
.其中正确的有( )
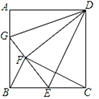
A. ①② B. ①②③ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
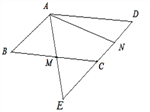
【题目】如图,在平行四边形ABCD中,M,N分别为BC,CD的中点,AM=1,AN=2,∠MAN=60°,AM ,DC的延长线相交于点E,则AB的长为_____________;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com