
 的中点,并证明你的结论.
的中点,并证明你的结论.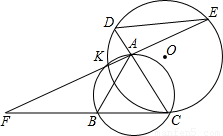
 ∠ABC=30°,那么∠BCD=∠BAF=30°,即可得解.
∠ABC=30°,那么∠BCD=∠BAF=30°,即可得解. 解:(1)连接KC;(1分)
解:(1)连接KC;(1分) ∠ABC=30°;(7分)
∠ABC=30°;(7分)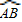 的中点.(9分)
的中点.(9分)

科目:初中数学 来源:1999年全国中考数学试题汇编《三角形》(03)(解析版) 题型:解答题
 个单位长度,Q的运动速度是
个单位长度,Q的运动速度是 个单位长度,运动到相遇时停止,设△OPQ的面积为S,运动时间为t秒,求S与t之间的函数关系式.
个单位长度,运动到相遇时停止,设△OPQ的面积为S,运动时间为t秒,求S与t之间的函数关系式.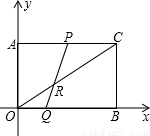
查看答案和解析>>
科目:初中数学 来源:1999年全国中考数学试题汇编《二次函数》(01)(解析版) 题型:解答题
 交x轴正半轴于A,B两点,交y轴于点C,且∠CBO=60°,∠CAO=45°,求抛物线的解析式和直线BC的解析式.
交x轴正半轴于A,B两点,交y轴于点C,且∠CBO=60°,∠CAO=45°,求抛物线的解析式和直线BC的解析式.
查看答案和解析>>
科目:初中数学 来源:1999年全国中考数学试题汇编《一次函数》(02)(解析版) 题型:解答题
 交x轴正半轴于A,B两点,交y轴于点C,且∠CBO=60°,∠CAO=45°,求抛物线的解析式和直线BC的解析式.
交x轴正半轴于A,B两点,交y轴于点C,且∠CBO=60°,∠CAO=45°,求抛物线的解析式和直线BC的解析式.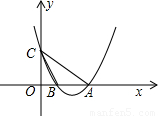
查看答案和解析>>
科目:初中数学 来源:1999年山东省烟台市中考数学试卷(解析版) 题型:解答题
 个单位长度,Q的运动速度是
个单位长度,Q的运动速度是 个单位长度,运动到相遇时停止,设△OPQ的面积为S,运动时间为t秒,求S与t之间的函数关系式.
个单位长度,运动到相遇时停止,设△OPQ的面积为S,运动时间为t秒,求S与t之间的函数关系式.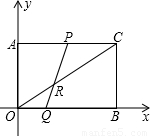
查看答案和解析>>
科目:初中数学 来源:1999年山东省烟台市中考数学试卷(解析版) 题型:解答题
 交x轴正半轴于A,B两点,交y轴于点C,且∠CBO=60°,∠CAO=45°,求抛物线的解析式和直线BC的解析式.
交x轴正半轴于A,B两点,交y轴于点C,且∠CBO=60°,∠CAO=45°,求抛物线的解析式和直线BC的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com