
分析 (1)将方程两边同时乘以$\frac{1}{2}$得到($\sqrt{2}$x-3)2=6,然后直接开平方法即可解得方程;
(2)由方程可知a=1,b=-6,c=-6,b2-4ac=36+24=60,然后利用求根公式即可解得方程;
(3)将原方程因式分解成(2x-13)(2x+13)=0,即可解得方程.
解答 解:(1)∵2($\sqrt{2}$x-3)2=12,
∴($\sqrt{2}$x-3)2=6,
∴$\sqrt{2}$x-3=±$\sqrt{6}$,
∴x1=$\frac{3\sqrt{2}}{2}$+$\sqrt{3}$,x2=$\frac{3\sqrt{2}}{2}$-$\sqrt{3}$;
(2)∵x2-6x-6=0,
∴a=1,b=-6,c=-6,b2-4ac=36+24=60,
∴x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{6±\sqrt{60}}{2}$=3±$\sqrt{15}$,
∴x1=3+$\sqrt{15}$,x2=3-$\sqrt{15}$;
(3)∵4x2-169=0,
∴(2x-13)(2x+13)=0,
∴x1=$\frac{13}{2}$,x2=-$\frac{13}{2}$.
点评 本题主要考查了解一元二次方程的知识,根据方程的特点选择合适的方法解一元二次方程是解决此类问题的关键.一般解一元二次方程的方法有直接开平方法、因式分解法、公式法、配方法.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知直线y=3-x交x轴于点A,交y轴于点B.双曲线y=$\frac{2}{x}$(x>0)与直线交于点C、点D.点P是双曲线上位于C、D两点之间的一动点,过点P作y 轴的垂线交y轴于点F,交直线与点N.过点P作x轴的垂线交x轴于点E,交直线于点M.则BM•AN的值为( )
如图,已知直线y=3-x交x轴于点A,交y轴于点B.双曲线y=$\frac{2}{x}$(x>0)与直线交于点C、点D.点P是双曲线上位于C、D两点之间的一动点,过点P作y 轴的垂线交y轴于点F,交直线与点N.过点P作x轴的垂线交x轴于点E,交直线于点M.则BM•AN的值为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=5x+5交x轴于点A,交y轴于点C,过A,C两点的二次函数y=ax2+4x+c的图象交x轴于另一点B.
如图,直线y=5x+5交x轴于点A,交y轴于点C,过A,C两点的二次函数y=ax2+4x+c的图象交x轴于另一点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
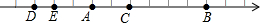 如图,图中数轴的单位长度为1.请回答下列问题:
如图,图中数轴的单位长度为1.请回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com