练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差: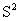

    甲

    乙

    丙

    丁

    平均数(cm)

    561

    560

    561

    560

    方差

    3.5

    3.5

    15.5

    16.5

    根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择

    A. 甲         B.乙        C.丙        D.丁


    A

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


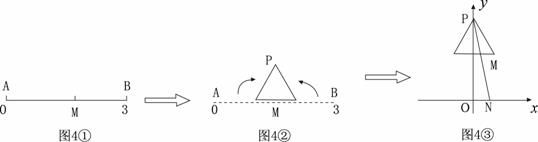
    在数轴上截取从0到3的对应线段AB，实数m对应AB上的点M，如图4①；将AB折成正三角形，使点A、B重合于点P，如图4②；建立平面直角坐标系，平移此三角形，使它关于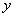轴对称，且点P的坐标为（0,2），PM的延长线与轴交于点N(n，0)，如图4③，当m=时，n的值为

       A．              B．         C．          D．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


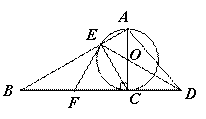
    已知如图，以Rt△ABC的AC边为直径作⊙O交斜边AB于点E，连接EO并延长交BC的延长线于点D，点F为BC的中点，连接EF

    （1）求证：EF是⊙O的切线；

    （2）若⊙O的半径为3，∠EAC＝60°，求AD的长。

     


      

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在“全民读书月”活动中，小明调查了班级里40名同学本学期计划购买课外书的花费情况，并将结果绘制成如图所示的统计图.请根据相关信息，解答下列问题：（直接填写结果）

    （1）这次调查获取的样本数据的众数是　  　   ；

    （2）这次调查获取的样本数据的中位数是　　   ；

    （3）若该校共有学生1000人，根据样本数据，估计本学期计划购买课外书花费50元的学生有　   　人．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


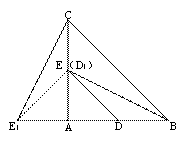
    在Rt△ABC中，∠A=90°，AC=AB=4， D，E分别是AB，AC的中点．若等腰Rt△ADE绕点A逆时针旋转，得到等腰Rt△AD1E1，设旋转角为α（0<α≤180°），记直线BD1与CE1的交点为P．

    （1）如图1，当α=90°时，线段BD1的长等于        ，线段CE1的长等于        ；（直接填写结果）

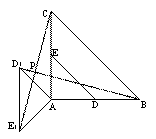
    （2）如图2，当α=135°时，求证：BD1= CE1，且BD1⊥CE1；

    （3）①设BC的中点为M，则线段PM的长为        ；②点P到AB所在直线的距离的最大值为        ．（直接填写结果）

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    直线y= -3x+5不经过的象限为_______________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    解分式方程:

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某班有20位同学参加围棋、象棋比赛，甲说：“只参加一项的人数大于14人。”乙说：“两项都参加的人数小于5人。”对于甲、乙两人的说法，有下列四个命题，其中真命题的是（ ）

    A.若甲对，则乙对 B.若乙对，则甲对 C.若乙错，则甲错 D.若甲粗，则乙对

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列图案中，轴对称图形是（      ）

     


     

    查看答案和解析>>

    同步练习册答案