
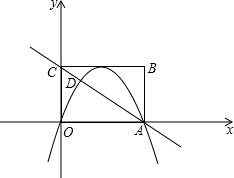
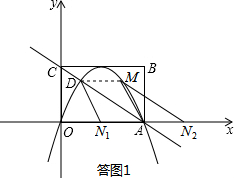
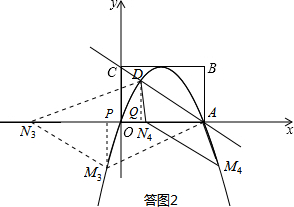
 (2013•昆明)如图,矩形OABC在平面直角坐标系xOy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O,A两点,直线AC交抛物线于点D.
(2013•昆明)如图,矩形OABC在平面直角坐标系xOy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O,A两点,直线AC交抛物线于点D.| 9 |
| 4 |
| 9 |
| 4 |
| 9 |
| 4 |
| 9 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
|
|
| 3 |
| 4 |
|
|
|
| 9 |
| 4 |
| 9 |
| 4 |
| 9 |
| 4 |
| 9 |
| 4 |
| 9 |
| 4 |
| 3 |
| 4 |
| 7 |
| 7 |
| 7 |
| 7 |
| 7 |
| 7 |
| 7 |
| 7 |


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:
 (2013•昆明)如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:
(2013•昆明)如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•昆明)如图,从直径为4cm的圆形纸片中,剪出一个圆心角为90°的扇形OAB,且点O、A、B在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是
(2013•昆明)如图,从直径为4cm的圆形纸片中,剪出一个圆心角为90°的扇形OAB,且点O、A、B在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是
| ||
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•昆明)如图,为了缓解交通拥堵,方便行人,在某街道计划修建一座横断面为梯形ABCD的过街天桥,若天桥斜坡AB的坡角∠BAD为35°,斜坡CD的坡度为i=1:1.2(垂直高度CE与水平宽度DE的比),上底BC=10m,天桥高度CE=5m,求天桥下底AD的长度?(结果精确到0.1m,参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
(2013•昆明)如图,为了缓解交通拥堵,方便行人,在某街道计划修建一座横断面为梯形ABCD的过街天桥,若天桥斜坡AB的坡角∠BAD为35°,斜坡CD的坡度为i=1:1.2(垂直高度CE与水平宽度DE的比),上底BC=10m,天桥高度CE=5m,求天桥下底AD的长度?(结果精确到0.1m,参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com