
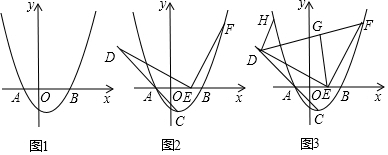
分析 (1)根据抛物线的对称轴x=1,AB=4,推出A(-1,0),B(3,0),推出顶点C坐标(1,-2),设抛物线的解析式为y=a(x-1)2-2,把(-1,0)代入得a=$\frac{1}{2}$,由此即可解决问题.
(2)如图1中,作DN⊥x轴于N,作FM⊥x轴于M,连接AF.只要证明△DEN≌△EFM,推出DN=EM,EN=FM,因为A(-1,0),C(1,-2),所以tan∠CAO=$\frac{2}{2}$=1,推出∠DAN=∠OAC=45°,推出DN=AN=EM,推出EN=AM=FM,推出∠FAM=45°,推出直线AF的解析式为y=x+1,由$\left\{\begin{array}{l}{y=x+1}\\{y=\frac{1}{2}{x}^{2}-x-\frac{3}{2}}\end{array}\right.$解方程组即可确定点F坐标.
(3)如图2中,作DN⊥x轴于N,FM⊥x轴于M,DJ⊥EG于J,延长EG使得EJ=JK,在EK的延长线上截取KP=DJ,作PQ⊥PE,截取PQ=KJ,连接DQ交抛物线于H.
只要证明∠HDF=2∠DEA,求得直线DQ的解析式为y=3x+15,解方程组:$\left\{\begin{array}{l}{y=3x+15}\\{y=\frac{1}{2}{x}^{2}-x-\frac{3}{2}}\end{array}\right.$即可解决问题.
解答 解:(1)对于抛物线y=ax2-2ax+b,对称轴x=-$\frac{-2a}{2a}$=1,
∵AB=4,
∴A(-1,0),B(3,0),顶点C坐标(1,-2),
设抛物线的解析式为y=a(x-1)2-2,把(-1,0)代入得a=$\frac{1}{2}$,
∴抛物线是解析式为y=$\frac{1}{2}$(x-1)2-2,即y=$\frac{1}{2}$x2-x-$\frac{3}{2}$,
∴a=$\frac{1}{2}$,b=-$\frac{3}{2}$.
(2)如图1中,作DN⊥x轴于N,作FM⊥x轴于M,连接AF.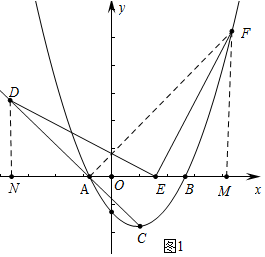
∵∠DNE=∠EMF=∠DEF=90°,
∴∠DEN+∠FEM=90°,∠FEM+∠EFM=90°,
∴∠DEN=∠EFM,
在△DEN和△EFM中,
$\left\{\begin{array}{l}{∠DEN=∠EFM}\\{∠DNE=∠EMF}\\{DE=EF}\end{array}\right.$,
∴△DEN≌△EFM,
∴DN=EM,EN=FM,
∵A(-1,0),C(1,-2),
∴tan∠CAO=$\frac{2}{2}$=1,
∴∠DAN=∠OAC=45°,
∴DN=AN=EM,
∴EN=AM=FM,
∴∠FAM=45°,
∴直线AF的解析式为y=x+1,
由$\left\{\begin{array}{l}{y=x+1}\\{y=\frac{1}{2}{x}^{2}-x-\frac{3}{2}}\end{array}\right.$解得$\left\{\begin{array}{l}{x=5}\\{y=6}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$,
∴点F的坐标为(5,6).
(3)如图2中,作DN⊥x轴于N,FM⊥x轴于M,DJ⊥EG于J,延长EG使得EJ=JK,在EK的延长线上截取KP=DJ,作PQ⊥PE,截取PQ=KJ,连接DQ交抛物线于H.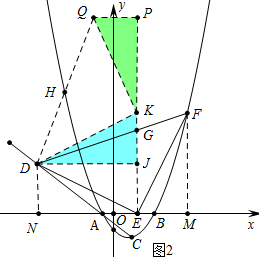
∵DN∥EG∥FM,DG=2FG,
∴$\frac{EN}{EM}$=$\frac{DG}{GF}$=2,
∴FM=EN=2EM,
∵FM=6,
∴DN=EM=EJ=KJ=3,DJ=EN=6,
∵DJ=PK=6,PQ=KJ=3,∠DJK=∠QPK,
∴△DJK≌△KPQ,
∴DK=KQ,∠KDJ=∠QKP,
∵∠KDJ+∠DKJ=90°,
∴∠DKJ+∠QKP=90°,
∴∠DKQ=90°,
∴∠KDQ=∠DQK=45°,
∵DK=DE,DJ⊥EK,
∠JDK=∠JDE=∠DEA,
∴∠KDE=2∠DEA=∠EDF+∠KDF=45°+∠KDF=∠QDK+∠KDG=∠QDF,
∴∠HDF=2∠DEA,
∵Q(-1,12),D(-4,3),
∴直线DQ的解析式为y=3x+15,
由$\left\{\begin{array}{l}{y=3x+15}\\{y=\frac{1}{2}{x}^{2}-x-\frac{3}{2}}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-3}\\{y=6}\end{array}\right.$或$\left\{\begin{array}{l}{x=11}\\{y=48}\end{array}\right.$,
∵点H在第二象限,
∴点H的坐标为(-3,6).
点评 本题考查二次函数综合题、一次函数的应用、全等三角形的判定和性质、等腰直角三角形的性质、锐角三角函数等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会构建一次函数,利用方程组求两个函数的交点坐标,本题体现了数形结合的思想,属于中考压轴题.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:解答题
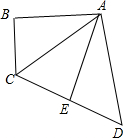 如图,在四边形ABCD中,∠B=90°,点E是CD的中点,连结AE,AC,且AC=AD,AB=AE.
如图,在四边形ABCD中,∠B=90°,点E是CD的中点,连结AE,AC,且AC=AD,AB=AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
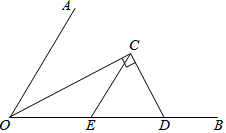 如图,∠AOB=60°,OC平分∠AOB,C为角平分线上一点,过点C作CD⊥OC,垂足为C,交OB于点D,CE∥OA交OB于点E.
如图,∠AOB=60°,OC平分∠AOB,C为角平分线上一点,过点C作CD⊥OC,垂足为C,交OB于点D,CE∥OA交OB于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.
如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.$\stackrel{•}{3}$$\stackrel{•}{4}$ | B. | $\frac{22}{7}$ | C. | $\sqrt{16}$ | D. | 0.020020002… |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB 为⊙O 的切线,切点为 B,连接 AO 与⊙O 交与点 C,BD 为⊙O 的直径,连接 CD,若∠A=30°,OA=2,则图中阴影部分的面积为( )
如图,AB 为⊙O 的切线,切点为 B,连接 AO 与⊙O 交与点 C,BD 为⊙O 的直径,连接 CD,若∠A=30°,OA=2,则图中阴影部分的面积为( )| A. | $\frac{π}{3}-\frac{{\sqrt{3}}}{4}$ | B. | $\frac{4π}{3}-2\sqrt{3}$ | C. | $π-\sqrt{3}$ | D. | $\frac{4}{3}π-\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)在如图所示的方格纸中,经过线段AB外一点C,画线段AB的垂线CH(垂足为H)和平行线EF.(画出的线请用铅笔描粗描黑)
(1)在如图所示的方格纸中,经过线段AB外一点C,画线段AB的垂线CH(垂足为H)和平行线EF.(画出的线请用铅笔描粗描黑)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com