
 如图,在△ABC中,AB=6,BC=AC=5.
如图,在△ABC中,AB=6,BC=AC=5.分析 (1)在直角△BCD中,由勾股定理可以求得CD的长度;
(2)利用面积法来求AE的长度;
(3)利用面积法来求DF的长度.
解答  解:(1)∵在△ABC中,AB=6,BC=AC=5,CD是高线,
解:(1)∵在△ABC中,AB=6,BC=AC=5,CD是高线,
∴BD=$\frac{1}{2}$AB=3,
∴在直角△BCD中,由勾股定理得到:CD=$\sqrt{B{C}^{2}-B{D}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4;
(2)∵$\frac{1}{2}$AB•CD=$\frac{1}{2}$BC•AE,
∴AE=$\frac{AB•CD}{BC}$=$\frac{6×4}{5}$=$\frac{24}{5}$.
(3)∵$\frac{1}{2}$BD•CD=$\frac{1}{2}$BC•DF,
∴DF=$\frac{BD•CD}{BC}$=$\frac{3×4}{5}$=$\frac{12}{5}$.
点评 本题考查了勾股定理、等腰三角形的性质.解答(2)(3)题时,利用了面积法来求三角形一边上的高线.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:解答题
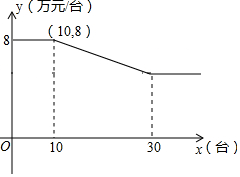 某公司销售智能机器人,售价每台为10万元,进价y与销售量x的函数关系如图所示.
某公司销售智能机器人,售价每台为10万元,进价y与销售量x的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
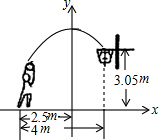 如图,运动员甲在距篮下4m处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5m时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.
如图,运动员甲在距篮下4m处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5m时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
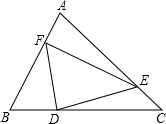 如图,若△DEF面积为a,且BF=2AF,CD=3BD,AE=4CE,则△ABC的面积为( )
如图,若△DEF面积为a,且BF=2AF,CD=3BD,AE=4CE,则△ABC的面积为( )| A. | 3a | B. | $\frac{12}{5}$a | C. | $\frac{4}{3}$a | D. | $\frac{8}{3}$a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com