练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    （2012•南京）下框中是小明对一道题目的解答以及老师的批改．
     题目：某村计划建造如图所示的矩形蔬菜温室，要求长与宽的比为2：1，在温室内，沿前侧内墙保留3m的空地，其他三侧内墙各保留1m的通道，当温室的长与宽各为多少时，矩形蔬菜种植区域的面积是288m2？
    解：设矩形蔬菜种植区域的宽为xm，则长为2xm，
    根据题意，得x•2x=288．
    解这个方程，得x1=-12（不合题意，舍去），x2=12
    所以温室的长为2×12+3+1=28（m），宽为12+1+1=14（m）
    答：当温室的长为28m，宽为14m时，矩形蔬菜种植区域的面积是288m2．我的结果也正确！
    小明发现他解答的结果是正确的，但是老师却在他的解答中画了一条横线，并打了一个？．

    结果为何正确呢？
    （1）请指出小明解答中存在的问题，并补充缺少的过程：
    变化一下会怎样…
    （2）如图，矩形A′B′C′D′在矩形ABCD的内部，AB∥A′B′，AD∥A′D′，且AD：AB=2：1，设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d，要使矩形A′B′C′D′∽矩形ABCD，a、b、c、d应满足什么条件？请说明理由．
    分析：（1）根据题意可得小明没有说明矩形蔬菜种植区域的长与宽之比为2：1的理由，所以应设矩形蔬菜种植区域的宽为xm，则长为2xm，然后由题意得方
    2y-3-1
    y-1-1
    =
    2y-4
    y-2
     =2    ，矩形蔬菜种植区域的长与宽之比为2：1，再利用小明的解法求解即可；
    （2）由使矩形A′B′C′D′∽矩形ABCD，利用相似多边形的性质，可得
    A′D′
    A′B′
    =
    AD
    AB
    ，即
    AD-(a+c)
    AB-(b+d)
    =
    2
    1
    ，然后利用比例的性质，即可求得答案．
    解答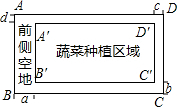：解：（1）小明没有说明矩形蔬菜种植区域的长与宽之比为2：1的理由．
    在“设矩形蔬菜种植区域的宽为xm，则长为2xm．”前补充以下过程：
    设温室的宽为ym，则长为2ym．
    则矩形蔬菜种植区域的宽为（y-1-1）m，长为（2y-3-1）m．
    ∵
    2y-3-1
    y-1-1
    =
    2y-4
    y-2
     =2    ，
    ∴矩形蔬菜种植区域的长与宽之比为2：1；

    （2）要使矩形A′B′C′D′∽矩形ABCD，
    就要
    A′D′
    A′B′
    =
    AD
    AB
    ，即
    AD-(a+c)
    AB-(b+d)
    =
    2
    1
    ，
    即
    2AB-(a+c)
    AB-(b+d)
    =
    2
    1
    ，
    即2AB-2（b+d）=2AB-（a+c），
    ∴a+c=2（b+d），
    即
    a+c
    b+d
    =2    ．
    点评：此题考查了相似多边形的性质．此题属于阅读性题目，注意理解题意，读懂题目是解此题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （2012•南京）如图，将45°的∠AOB按下面的方式放置在一把刻度尺上：顶点O与尺下沿的端点重合，OA与尺下沿重合，OB与尺上沿的交点B在尺上的读数恰为2cm．若按相同的方式将37°的∠AOC放置在该刻度尺上，则OC与尺上沿的交点C在尺上的读数约为
    2.7
    2.7
    cm．（结果精确到0.1cm，参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•南京二模）端午节期间，某食品店平均每天可卖出300只粽子，卖出1只粽子的利润是1元．经调查发现，零售单价每降0.1元，每天可多卖出100只粽子．为了使每天获取的利润更多，该店决定把零售单价下降m（0＜m＜1）元．
    （1）零售单价下降m元后，该店平均每天可卖出
    300+100×
    m
    0.1
    300+100×
    m
    0.1
    只粽子，利润为
    （1-m）（300+100×
    m
    0.1
    ）
    （1-m）（300+100×
    m
    0.1
    ）
    元．
    （2）在不考虑其他因素的条件下，当m定为多少时，才能使该店每天获取的利润是420元并且卖出的粽子更多？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•南京二模）在显微镜下，一种细胞的截面可以近似地看成圆，它的半径约为5×10-7m，若π≈3.14，则这种细胞的截面面积用科学记数法表示大约是（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    下表是我省气象台对2012年5月1日最高温度（单位：℃）的预报，当天预报最高温度数据的众数是
    24
    24
    ．
    城市 南京 徐州 连云港 淮安 盐城 宿迁 扬州 泰州 镇江 常州 无锡 苏州 南通
    最高
    温度    		 24 21 22 22 22 20 25 30 26 25 24 24 24

    查看答案和解析>>

    同步练习册答案