
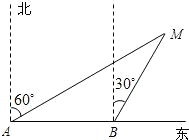
 某渔船上的渔民在A处观测到灯塔M在北偏东60°方向处,这艘渔船以每小时40海里的速度向正东方向航行,1小时后到达B处,在B处观测到灯塔M在北偏东30°方向处.则B处与灯塔的距离BM是40海里.
某渔船上的渔民在A处观测到灯塔M在北偏东60°方向处,这艘渔船以每小时40海里的速度向正东方向航行,1小时后到达B处,在B处观测到灯塔M在北偏东30°方向处.则B处与灯塔的距离BM是40海里. 分析 先根据题中角之间的关系证△ABM是等腰三角形,则BM=AB,然后把BM放到直角三角形中,利用30°或60°角,解三角形即可.
解答 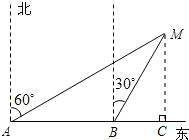 解:过点M作直线AB的垂线MC,垂足为C,设CM=x海里,
解:过点M作直线AB的垂线MC,垂足为C,设CM=x海里,
在Rt△AMC中,AC=$\sqrt{3}$x;在Rt△BMC中,BC=$\frac{\sqrt{3}}{3}$x
由于AC-BC=AB得:$\sqrt{3}$x-$\frac{\sqrt{3}}{3}$x=40,
解得:x=20$\sqrt{3}$,BC=$\frac{\sqrt{3}}{3}$x=20,
在Rt△BMC中,BM=2BC.
答:灯塔B与渔船M的距离是40海里.
故答案为:40.
点评 本题考查了解直角三角形的应用-方向角问题.解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
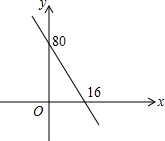 某汽车销售公司销售某种型号的汽车,每辆车进价6万元,售价为x万元,经市场调查发现销售量y与销售价x的关系如图.
某汽车销售公司销售某种型号的汽车,每辆车进价6万元,售价为x万元,经市场调查发现销售量y与销售价x的关系如图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com