解:(1)第4行的各数分别为:1+2
4,2+2
4,2
2+2
4,2
3+2
4;
故答案为:1+2
4,2+2
4,2
2+2
4,2
3+2
4.
(2)根据规律,第n行的数为:1+2
n,2+2
n,2
2+2
n,…,2
n-1+2
n,
∵第1行有1个数,第2行有2个数,第3行有3个数,…,第n行有n个数,
∴1+2+3+…+n=

,
令

=15,则n
2+n-30=0,
解得n
1=5,n
2=-6(舍去),
∴第15个数是第5行的第5个数,为2
4+2
5=16+32=48;
(3)当n=10时,

=

=55,
所以,第55个数是第10行的最后一个数,为2
9+2
10=512+1024=1536.
分析:(1)根据规律,第4行共有4个算式,每一个算式的第二个加数都是2
4,第一个加数按照从左到右的顺序依次为1、2、2
2、2
3,写出即可;
(2)根据规律写出第n行的数的通项表达式,再根据每一行的数的个数与行数相同,求出第15个数是第5行的最后一个数,然后把n=5代入进行计算即可得解;
(3)求出第55个数所在的行数与位置,然后进行计算即可得解.
点评:本题是对数字变化规律的考查,规律性较强,难度较大,根据指数的变化特点写出第n行排列的各数是解题的关键.

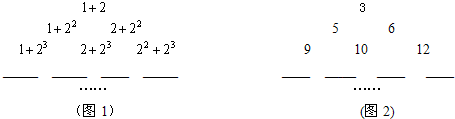
 ,
, =15,则n2+n-30=0,
=15,则n2+n-30=0, =
= =55,
=55,

