
已知一个底面为菱形的直棱柱,高为 10 c
10 c m,体积为150 cm3,则这个棱柱下底面积为______cm2; 若该棱柱侧面展开图的面积为200 cm2,记底面菱形的顶点依次为A,B,C,D,AE是BC边上的高,则CE的长为______cm.
m,体积为150 cm3,则这个棱柱下底面积为______cm2; 若该棱柱侧面展开图的面积为200 cm2,记底面菱形的顶点依次为A,B,C,D,AE是BC边上的高,则CE的长为______cm.
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
有三张正面分别写有数-2 ,-1,1的卡片,它们的背面完全相同,将这三张卡片背面朝上洗匀后随机抽取一张,以其正面的数作为x的值,放回卡片洗匀,再从三张卡片中随机抽取一张,以其正面的数作为y的值,两次结果记为(x,y).
(1)用画树状图法或列表法表示(x,y)所有可能出现的结果;
(2)求使代数式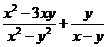 有意义的(x,y)出现的概率;
有意义的(x,y)出现的概率;
(3)化简代数式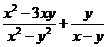 ,并求使代数式的值为整数的(x,y)出现的概率.
,并求使代数式的值为整数的(x,y)出现的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
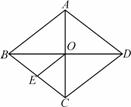
如图,菱形ABCD中,对角线AC与BD相交于O,OE∥DC且交BC于点E,AD=6 cm,则OE的长为( )
A.6 cm B.4 cm C.3 cm D.2 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
勾股定理是几何中的一个重要定理, 在我国古算书《周髀算经》中就有“若勾三,股四,则弦五
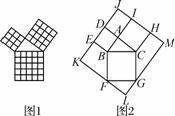
在我国古算书《周髀算经》中就有“若勾三,股四,则弦五 ”的记载,如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积验证勾股定理,图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为( )
”的记载,如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积验证勾股定理,图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为( )
A.90 B.100 C.110 D.121
查看答案和解析>>
科目:初中数学 来源: 题型:
有七张正面分别标有数字-3,-2,-1,0,1,2,3的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为a,则使 关于x的一元二次方程x2-2(a-1)x+a(a-3)=0有两个不相等的实数根,且以x为自变量的二次函数y=x2-(a2+1)x-a+2的图象不经过点(1,0)的概率是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com