解法一:(1)证明:连接AC交BD于点O
∵四边形ABCD为菱形
∴AC⊥BD,BO=OD
∵AE⊥AD
∴△AOD∽△EAD
∴
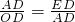
∴AD
2=OD×ED
∴AD
2=

DE×BD
(2)解:解方程x
2-3mx+2m
2=0得x
1=m,x
2=2m
∵BE<DE
∴BE=m,DE=2m
∵AD
2=

DE×BD
∴AD=

m
在Rt△BEF中,DE=2m,AD=

m
∴AE=m,∠ADB=30°
在Rt△ADE中,∠EBF=30°,BE=m
∴EF=

m,∴AF=

m
∵S
ABCD=AD×AF=

m×

m=6

∴m
2=4
∴m=±2(负值舍去)
∴m=2
∵EG⊥AF,AD⊥AF
∴GE∥AD
∴
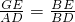
∴GE=

解法二:(1)证:取DE的中点G
在Rt△EAD中,AG=DG=EG
∴∠GAD=∠GDA
∵四边形ABCD为菱形
∴AB=AD
∴∠ABD=∠ADB
∴∠GAD=∠ABD,∠ADB=∠ADB
∴△ADG∽△BDA
∴
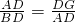
∴AD2=DG×BD=

DE×BD
(2)解:∵x
2-3mx+2m
2=0
∴x
1=m,x
2=2m
∵BE<DE
∴BE=m,DE=2m
∵AD2=

DE×BD
∴AD=

m
Rt△AOD中,AD=

m,OD=

m,
∴AO=

m,
∴AC=

m
∵S
ABCD=

AC×BD=

×

m×3m=6

∴m
2=4,∴m=±2(负值舍去)
∴m=2
∵EG⊥AE,AD⊥AF
∴GE∥AD
∴
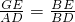
∴GE=

分析:(1)连接AC交BD于O,根据菱形的性质可得到△AOD∽△EAD,根据相似三角形的对应边成比例即可得到结果;
(2)先解二次方程,求出BE,DE的值,直接利用(1)的结果,可求出AD的值,再利用勾股定理及三角函数求得AE,EF,BF的值,根据比例线段求得EG的长,再根据菱形的面积可求出m的值,那么EG就求出来了.
点评:本题考查菱形的性质、勾股定理,解一元二次方程的理解及运用.

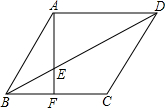 已知:如图,四边形ABCD为菱形,AF⊥AD交BD于点E,交BC于点F.
已知:如图,四边形ABCD为菱形,AF⊥AD交BD于点E,交BC于点F. DE•DB;
DE•DB; ,求EG的长.
,求EG的长.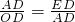
 DE×BD
DE×BD DE×BD
DE×BD m
m m
m m,∴AF=
m,∴AF= m
m m×
m× m=6
m=6
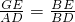

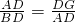
 DE×BD
DE×BD DE×BD
DE×BD m
m m,OD=
m,OD= m,
m, m,
m, m
m AC×BD=
AC×BD= ×
× m×3m=6
m×3m=6
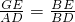



 轻松暑假总复习系列答案
轻松暑假总复习系列答案 已知:如图,四边形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四边形ABCD绕直线AB旋转一周,则所得几何体的表面积是多少?
已知:如图,四边形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四边形ABCD绕直线AB旋转一周,则所得几何体的表面积是多少?