解:(1)∵∠ACB=90°,∠A=30°,
∴∠B=60°,
∵点D是AB的中点,
∴DB=DC,
∴△DCB为等边三角形,
∵DE⊥BC,
∴DE=

BC;
故答案为DE=

BC.
(2)BF+BP=

DE.理由如下:
∵线段DP绕点D逆时针旋转60°,得到线段DF,
∴∠PDF=60°,DP=DF,
而∠CDB=60°,
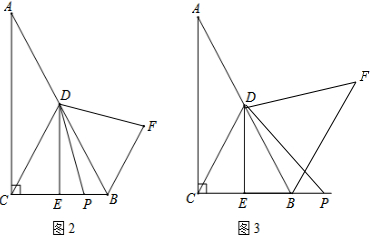
∴∠CDB-∠PDB=∠PDF-∠PDB,
∴∠CDP=∠BDF,
在△DCP和△DBF中
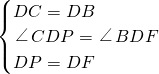
,
∴△DCP≌△DBF(SAS),
∴CP=BF,
而CP=BC-BP,
∴BF+BP=BC,
∵DE=

BC,
∴BC=

DE,
∴BF+BP=

DE;
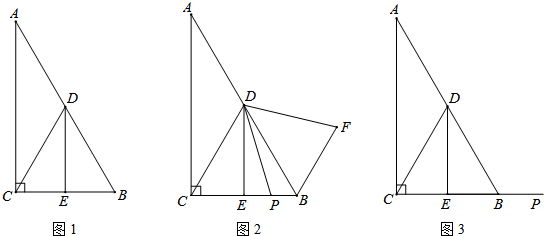
(3)如图,
与(2)一样可证明△DCP≌△DBF,
∴CP=BF,
而CP=BC+BP,
∴BF-BP=BC,
∴BF-BP=

DE.
分析:(1)由∠ACB=90°,∠A=30°得到∠B=60°,根据直角三角形斜边上中线性质得到DB=DC,则可判断△DCB为等边三角形,由于DE⊥BC,DE=

BC;
(2)根据旋转的性质得到∠PDF=60°,DP=DF,易得∠CDP=∠BDF,则可根据“SAS”可判断△DCP≌△DBF,则CP=BF,利用CP=BC-BP,DE=

BC可得到BF+BP=

DE;
(3)与(2)的证明方法一样得到△DCP≌△DBF得到CP=BF,而CP=BC+BP,则BF-BP=BC,所以BF-BP=

DE.
点评:本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.也考查了等边三角形的判定与性质以及含30度的直角三角形三边的关系.

 BC;
BC; BC.
BC. DE.理由如下:
DE.理由如下:
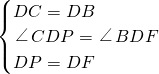 ,
, BC,
BC, DE,
DE, DE;
DE; DE.
DE. BC;
BC; BC可得到BF+BP=
BC可得到BF+BP= DE;
DE; DE.
DE.
