
 如图,若∠C=90°,AD=DB,ED⊥AB,AB=20,AC=12,则四边形ADEC的面积为
如图,若∠C=90°,AD=DB,ED⊥AB,AB=20,AC=12,则四边形ADEC的面积为 ,在Rt△ADE中,由勾股定理求出DE=
,在Rt△ADE中,由勾股定理求出DE= ,根据四边形ADEC的面积S=S△ACE+S△ADE代入求出即可.
,根据四边形ADEC的面积S=S△ACE+S△ADE代入求出即可. 解:连接AE.
解:连接AE. ,
, AB=10,
AB=10, =
= ,
, ×12×(16-
×12×(16- )+
)+ ×10×
×10× =58.5.
=58.5.

科目:初中数学 来源: 题型:
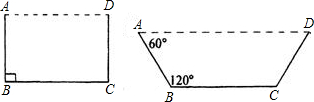 面积更大.画出你设计的草图,标上必要的数据(不要求写出解答过程).
面积更大.画出你设计的草图,标上必要的数据(不要求写出解答过程).查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源:2007年湖北省武汉市中考数学试卷(解析版) 题型:解答题
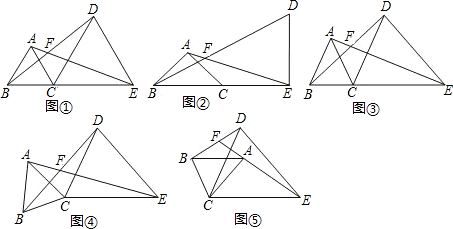
 ;在图⑤中,∠AFB与∠α的数量关系是______.请你任选其中一个结论证明.
;在图⑤中,∠AFB与∠α的数量关系是______.请你任选其中一个结论证明.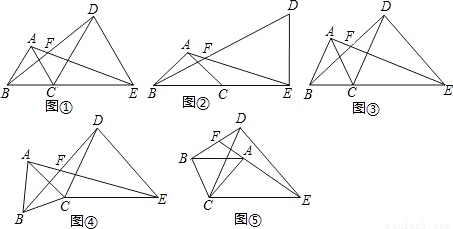
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com