
����Ŀ���ڵ���ֱ��������ABC�У�AB=AC����BAC=90�㣮��PΪֱ��AB��һ�����㣨��P�����A��B�غϣ�������PC����D��ֱ��BC�ϣ���PD=PC������P��PE^PC����D��E��ֱ��AC��ͬ�࣬��PE=PC������BE��
��1�����һ������P���߶�AB��ʱ��ͼ����ͼ1 ��ʾ��
���������ͼ2������P��BA���ӳ����ϣ���AP��ABʱ���������ⲹȫͼ2����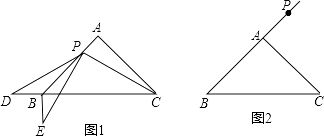
��2��������⣨1������������У���ѡһ�����������������⣺
����֤����ACP=��DPB��
���õ�ʽ��ʾ�߶�BC��BP��BE֮���������ϵ����֤����
���𰸡�
��1��
�⣺��ȫͼ����ͼ����ʾ
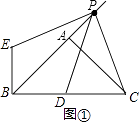
��2��
�⣺���һ��
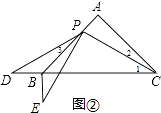
��֤������ͼ�ڣ�
��AB=AC����BAC=90�㣬
���ABC=��ACB=45�㣬
��PD=PC��
���1=��D��
�ߡ�ACB=��1+��2=45�㣬��ABC=��D+��=45�㣬
���3=��2��
����ACP=��DPB��
��BC= ![]() BP+BE�����ɣ�
BP+BE�����ɣ�
֤������ͼ�۹�P��PF��PB��BC��F��
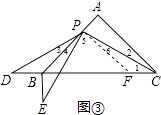
��PF��PB��
���BPF=90�㣬
��EP��PC��
���EPC=90�㣬
���4+��5=��6+��5��
���4=��6��
�ߡ�PBF=45�㣬
���PBF=��PFB=45�㣬
��PB=PF��
�ڡ�PBE���PFC�У�
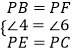 ��
��
���PBE�ա�PFC��
��BE=FC��
��BF= ![]() BP��
BP��
��BC=BF+FC= ![]() BP+BE��
BP+BE��
�����������ͼ�ܣ�
��PD=PC��
���PDC=��PCD��
�ߡ�ABC=��ACB=45�㣬
���3=��PDC��45�㣬��ACP=��PCD��45��
�����BPD=��ACP��
����ͼ�ܣ���P��PF��PB��BC��F��
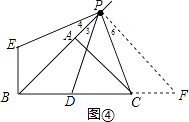
��PF��PB��
���BPF=90�㣬
��EP��PC��
���EPC=90�㣬
���4+��BPC=��6+��BPC=90�㣬
���4=��6��
�ߡ�PBF=45�㣬
���PBF=��PFB=45�㣬
��PB=PF��
�ڡ�PBE���PFC�У�
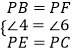 ��
��
���PBE�ա�PFC��
��BE=FC��
��BF= ![]() BP��
BP��
��BC=BF��FC= ![]() BP��BE��
BP��BE��
����������1���������ⲹȫͼ�μ��ɣ���2�����һ���ٸ��ݵ���ֱ�������ε����ʵõ���ABC=��ACB=45�㣬�ɵ��������ε����ʵõ���1=��D���������ε���ǵ����ʼ��ɵõ����ۣ��ڸ�����ǵ����ʵõ���4=��6���ɵ���ֱ�������ε����ʵõ���PBF=��PFB=45�㣬���ǵõ�PB=PF������ȫ�������ε����ʵõ�BE=FC���ɹ��ɶ����õ�BF= ![]() BP�����ɵõ����ۣ�
BP�����ɵõ����ۣ�
��������٣����ݵ��������ε����ʵõ���PDC=��PCD���ɡ�ABC=��ACB=45�㣬���ǵõ���3=��PDC��45�㣬��ACP=��PCD��45�㣬���ɵõ����ۣ�������ǵ����ʵõ���4=��6�����ݵ���ֱ�������ε����ʵõ���PBF=��PFB=45�㣬���ǵõ�PB=PF������ȫ�������ε����ʵõ�BE=FC�����ݹ��ɶ����õ�BF= ![]() BP���ǵõ����ۣ�
BP���ǵõ����ۣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AD��BC��D �� �����������١�B+��DAC=90�㣻�ڡ�B=��DAC���� ![]() =
= ![]() ����AB2=BDBC �� ����һ���ܹ��ж���ABC��ֱ�������ε��У�������
����AB2=BDBC �� ����һ���ܹ��ж���ABC��ֱ�������ε��У������� 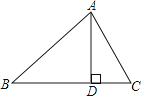
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
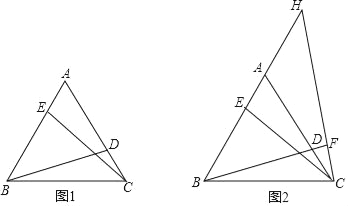
����Ŀ��(1)��ͼ1����D��E�ֱ��ǵȱ���ABC��AC��AB�ϵĵ㣬����BD��CE����AE=CD����֤��BD=CE.
(2)��ͼ2����(1)�ʵ������£���H��BA���ӳ����ϣ�����CH��BD�ӳ����ڵ�F.��BF=BC��
����֤��EH=EC��
�������ҳ��߶�AH��AD��DF֮���������ϵ����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽������y=x+ ![]() ��ͼ��������
��ͼ��������
��1������y=x+ ![]() ���Ա���x��ȡֵ��Χ����
���Ա���x��ȡֵ��Χ����
��2�������ĸ�����ͼ���У�����y=x+ ![]() ��ͼ�������
��ͼ�������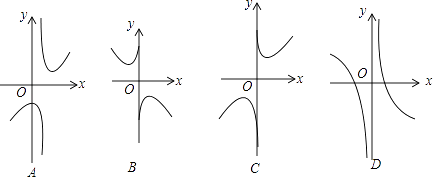
��3�����ں���y=x+ ![]() ����x��0ʱ��y��ȡֵ��Χ��
����x��0ʱ��y��ȡֵ��Χ��
�뽫������������Ĺ��̲���������
�⣺��x��0
��y=x+ ![]()
=�� ![]() ��2+��
��2+�� ![]() ��2
��2
=�� ![]() ��
�� ![]() ��2+
��2+
�ߣ� ![]() ��
�� ![]() ��2��0��
��2��0��
��y ��
��4��������y= ![]() ����y��ȡֵ��Χ��
����y��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�����������y1= ![]() ��ͼ����һ�κ���y2=ax+b��ͼ���ڵ�A��1��3����B����3��m����
��ͼ����һ�κ���y2=ax+b��ͼ���ڵ�A��1��3����B����3��m����
��1����������y1= ![]() ��һ�κ���y2=ax+b�ı���ʽ��
��һ�κ���y2=ax+b�ı���ʽ��
��2����C ������ƽ����һ�㣬BC��x �ᣬAD��BC ��ֱ��BC �ڵ�D������AC����AC= ![]() CD�����C�����꣮
CD�����C�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�У�AB=AC����A=30�㣬��BΪԲ�ģ�BC��Ϊ�뾶�������ֱ�AC��AB��D��E���㣬������BD��DE�� ���BDE�Ķ���Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB�ǡ�O��ֱ������H�ڡ�O�ϣ�E�� ![]() ���е㣬����E��EC��AH����AH���ӳ����ڵ�C������AE������E��EF��AB�ڵ�F��
���е㣬����E��EC��AH����AH���ӳ����ڵ�C������AE������E��EF��AB�ڵ�F��
��1����֤��CE�ǡ�O�����ߣ�
��2����FB=2��tan��CAE= ![]() ����OF�ij���
����OF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߶�AC��ֱ��l�ֱ�ֱ�߶�AB�ڵ�A��B����P���߶�AB�ϵ�һ�����㣬��A�ƶ���B������CP������P��PD��CP��l�ڵ�D�����߶�AP�ij�Ϊx��BD�ij�Ϊy��������ͼ���У��ܴ��±�ʾy��x֮�亯����ϵ���ǣ� ��
A.
B.
C.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=x2+bx+c��x�ύ��A��B���㣬B������Ϊ��3��0������y�ύ�ڵ�C��0����3��
��1���������ߵĽ���ʽ��
��2����P��������λ�ڵ������IJ������˶������ı���ABPC��������ʱ�����P��������ı���ABPC����������
��3��ֱ��l����A��C���㣬��Q��������λ��y�����IJ������˶���ֱ��m������B�͵�Q���Ƿ����ֱ��m��ʹ��ֱ��l��m��x��Χ�ɵ������κ�ֱ��l��m��y��Χ�ɵ����������ƣ������ڣ����ֱ��m�Ľ���ʽ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com