练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．为节约用水，某市对居民用水规定如下：大户（家庭人口4人及4人以上者）每月用水15m3以内的，小户（家庭人口3人及3人以下者）每月用水10m3以内的，按每立方米收取4.8元的水费；超过上述用量的，超过部分每立方米水费加倍收取．某用户5口人，本月实际用水25m3，则这户本月应交水费多少元？

    分析 根据用水的收费标准列出算式，计算即可得到结果．

    解答 解：根据题意得：15×4.8+（25-15）×4.8×2=72+96=168（元），
    答：这户本月应交水费168元．

    点评 此题考查了有理数的混合运算，弄清题中的收费标准是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

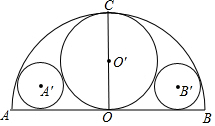    7．已知：如图，以AB为直径作半圆，半径OC⊥AB，以OC为直径作⊙OO′，再作⊙A′和⊙B都与AB、⊙O及⊙O′相切，如果AB=2R，求⊙A′的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

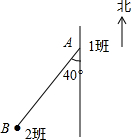    5．如图，在一次活动中，位于A处的1班准备前往相距5千米的B处与2班会合，请用方向和距离描述2班相对1班的位置：2班在1班的南偏西40°方向，距离A5千米的B处；反过来，请用方向和距离描述1班相对2班的位置：1班在2班的北偏东40°方向，距离B5千米的A处．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．手工课上，老师将同学们分成A，B两个小组制作两个汽车模型，每个模型先由A组同学完成打磨工作，再由B组同学进行组装完成制作，两个模型每道工序所需时间如表：则这两个模型都制作完成所需的最短时间为22分钟．
    工序
    时间
    模型    		打磨（A组）组装（B组）
    模型甲9分钟5分钟
    模型乙6分钟11分钟

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．某种品牌牛奶包装盒的表面展开图如图所示（单位：mm），那么这种牛奶包装盒的容积是2.24×105mm3（包装材料厚度不计）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．定义：f （a，b）=（-a，b），g（m，n）=（m，-n），例 f （1，2）=（-1，2），g（-4，-5）=（-4，5），则 g（ f （2，-3））=（-2，3）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．下列各式正确的有（　　）
    （1）$\frac{-a-b}{c-d}=\frac{a+b}{-c+d}$；（2）$\frac{-a-b}{c+d}=\frac{a+b}{c+d}$；（3）$\frac{-a-b}{c-d}=\frac{a+b}{-c-d}$；（4）$\frac{-a-b}{c-d}=\frac{-a-b}{c+d}$．
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．将抛物线y=3x2向右平移2个单位，再向下平移1个单位，所得抛物线的解析式为y=（x-2）2-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．研究几何图形，我们往往先给出这类图形的定义，再研究它的性质和判定方法．
    我们给出如下定义：
    如图，四边形ABCD中，AB=AD，CB=CD像这样两组邻边分别相等的四边形叫做“筝形”；
    小文根据学习几何图形的经验，通过观察、实验、归纳、类比、猜想、证明等方法，对AB≠BC的“筝形”的性质和判定方法进行了探究．下面是小文探究的过程，请补充完成：
    （1）他首先发现了这类“筝形”有一组对角相等，并进行了证明，请你完成小文的证明过程．
    已知：如图，在”筝形”ABCD中，AB=AD，CB=CD．求证：∠ABC=∠ADC．
    （2）小文由（1）得到了这类“筝形”角的性质，他进一步探究发现这类“筝形”还具有其它性质，请再写出这类“筝形”的一条性质（除“筝形”的定义外）“筝形”有一条对角线平分一组对角或“筝形”是轴对称图形
    （3）继性质探究后，小文探究了这类“筝形”的判定方法，写出这类“筝形”的一条判定方法（除“筝形”的定义外）：有一条对角线垂直平分另一条对角线的四边形是筝形．

    查看答案和解析>>

    同步练习册答案