
 )、B(6,0)两点同时出发,点O为坐标原点,甲
)、B(6,0)两点同时出发,点O为坐标原点,甲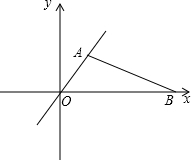 沿AO方向、乙沿BO方向均以4km/h的速度行驶,th后,甲到达M点,乙到达N点.
沿AO方向、乙沿BO方向均以4km/h的速度行驶,th后,甲到达M点,乙到达N点.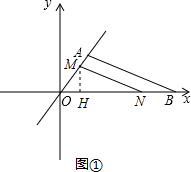 证明:(1)因为A坐标为(1,
证明:(1)因为A坐标为(1, ),
),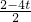 =
=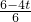 时,解得t=0,
时,解得t=0, ,乙达到O点的时间为t=
,乙达到O点的时间为t= =
= ,所以甲先到达O点,所以t=
,所以甲先到达O点,所以t= 或t=
或t= 时,O、M、N三点不能连接成三角形,
时,O、M、N三点不能连接成三角形, 时,如果△OMN∽△OBA,则有
时,如果△OMN∽△OBA,则有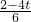 =
= ,解得t=2>
,解得t=2> ,所以,△OMN不可能相似△OBA;
,所以,△OMN不可能相似△OBA; <t≤
<t≤ 时,∠MON>∠AOB,显然△OMN不相似△OBA;
时,∠MON>∠AOB,显然△OMN不相似△OBA; 时,
时,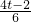 =
=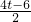 ,解得t=2>
,解得t=2> ,所以当t=2时,△OMN∽△OBA;
,所以当t=2时,△OMN∽△OBA; 时,如图1,过点M作MH⊥x轴,垂足为H,
时,如图1,过点M作MH⊥x轴,垂足为H, =
= (1-2t),
(1-2t), =1-2t,
=1-2t,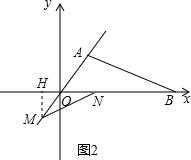
 (1-2t)]2+(5-2t)2=16t2-32t+28
(1-2t)]2+(5-2t)2=16t2-32t+28 <t≤
<t≤ 时,如图2,作MH⊥x轴,垂足为H,
时,如图2,作MH⊥x轴,垂足为H, (4t-2)=
(4t-2)= (2t-1),NH=
(2t-1),NH= (4t-2)+(6-4t)=5-2t,
(4t-2)+(6-4t)=5-2t, (1-2t)]2+(5-2t)2=16t2-32t+28
(1-2t)]2+(5-2t)2=16t2-32t+28 时,同理可得s=[
时,同理可得s=[ (1-2t)]2+(5-2t)2=16t2-32t+28,
(1-2t)]2+(5-2t)2=16t2-32t+28, (1-2t)]2+(5-2t)2=16t2-32t+28.
(1-2t)]2+(5-2t)2=16t2-32t+28. km.
km.

科目:初中数学 来源: 题型:
 如图,甲、乙两人分别从正方形ABCD的顶点C,B两点同时出发,甲由C向D运动,乙由B向C运动.若一人达到目的地,另一人随之停止,甲的速度为1千米/分,乙的速度为2千米/分.正方形的周长为40千米,问几分钟后,两人相距2
如图,甲、乙两人分别从正方形ABCD的顶点C,B两点同时出发,甲由C向D运动,乙由B向C运动.若一人达到目的地,另一人随之停止,甲的速度为1千米/分,乙的速度为2千米/分.正方形的周长为40千米,问几分钟后,两人相距2| 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
 沿AO方向、乙沿BO方向均以4km/h的速度行驶,th后,甲到达M点,乙到达N点.
沿AO方向、乙沿BO方向均以4km/h的速度行驶,th后,甲到达M点,乙到达N点.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,甲、乙两人分别从长正方形广场ABCD的顶点B、C同时出发,甲由C点向D点运动,乙由B点向C点运动,甲的速度1米/秒;乙的速度为2米/秒.若正方形的周长为400米,问几秒后,两人第一次相距20
如图,甲、乙两人分别从长正方形广场ABCD的顶点B、C同时出发,甲由C点向D点运动,乙由B点向C点运动,甲的速度1米/秒;乙的速度为2米/秒.若正方形的周长为400米,问几秒后,两人第一次相距20| 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com