我们常用各种多边形地砖铺砌成美丽的图案,也就是说,使用给定的某些多边形,能够拼成一个平面图形,既不留下一丝空白,又不互相重叠(在几何里称为平面密铺).当围绕一点拼在一起的几个多边形的内角和为360°时,就能够拼成一个平面图形.
探究用同一种正多边形进行平面密铺.
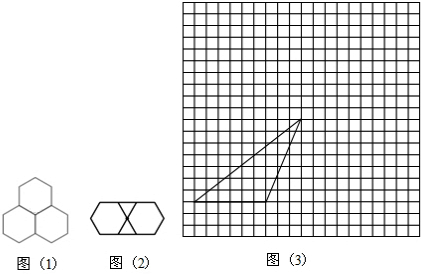
例如:如图1,用三个同种类型(大小一样、形状相同)的正六边形地砖可以平面密铺.
(1)请问仅限于同一种类型的多边形进行密铺,哪几种能平面密铺?
①②
①②
(填序号);
①正三角形 ②正四边形 ③正五边形 ④正八边形
探究用两种边长相等的正多边形进行平面密铺.
例如:如图2,二个正三角形和二个正六边形可以平面密铺.
(2)限用两种边长相等的正多边形进行平面密铺,以下哪几种是可行的?
ABE
ABE
A.正三角形和正方形 B.正方形和正八边形 C.正方形和正五边形
D.正八边形和正六边形 E.正三角形和正十二边形 F.正三角形和正五边形
(3)继续推广到用三种不同的正多边形进行平面密铺,请写出符合题意的不同组合.
例如:①正三角形、正方形、正六边形;
②正三角形、正九边形、正十八边形;
③
正三角形、正四边形,正十二边形
正三角形、正四边形,正十二边形
;
④
正三角形,正十边形,正十五边形
正三角形,正十边形,正十五边形
.
(4)如果用形状,大小相同的如图3方格纸中的三角形,能进行平面密铺吗?若能,请在方格纸中画出密铺的设计图.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案