

分析 (1)根据角平分线的性质可得∠BAE=∠EAD,根据平行线的性质可得∠AEB=∠EAD,等量代换即可求解;
(2)①先证明四边形ABCD是平行四边形,再根据平行四边形的性质即可求解;
②根据∠ADE=3∠CDE,设∠CDE=x°,∠ADE=3x°,∠ADC=2x°,根据平行线的性质得出方程90-x+60+3x=180,求出x即可.
解答 (1)证明:∵AE平分∠BAD,
∴∠BAE=∠EAD,
∵AD∥BC,
∴∠AEB=∠EAD,
∴∠BAE=∠BEA;
(2)①证明:∵AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形,
∴∠ABC=∠ADC;
②解:∵∠ADE=3∠CDE,设∠CDE=x°,
∴∠ADE=3x°,∠ADC=2x°,
∵AB∥CD,
∴∠BAD+∠ADC=180°,
∴∠DAB=180°-2x°,
∵∠DAE=∠BAE=∠BEA=90°-x°,
又∵AD∥BC,
∴∠BED+∠ADE=180°,
∵∠AED=60°,
即90-x+60+3x=180,
∴∠CDE=x°=15°,∠ADE=45°,
∵AD∥BC,
∴∠CED=180°-∠ADE=135°.
点评 本题考查了平行线的性质和判定的应用,用了方程的思想,能运用平行线的性质和判定进行推理是解此题的关键.


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>$\frac{1}{2}$ | B. | x≠$\frac{1}{2}$ | C. | x≥0且x≠$\frac{1}{2}$ | D. | x≥$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2x-y)2=4x2-2xy+y2 | B. | (a-b)2=(b-a)2 | ||
| C. | ($\frac{1}{2}$a-b)2=$\frac{1}{4}$a2+ab+b2 | D. | (x+2y)2=x2+4y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 车库的电动门栏杆如图所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD的大小是( )
车库的电动门栏杆如图所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD的大小是( )| A. | 150° | B. | 180° | C. | 270° | D. | 360° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
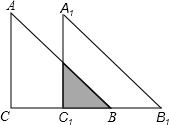 如图,Rt△ABC中∠C=90°,AC=BC=4,将△ABC沿CB方向移动到△A1B1C1的位置,
如图,Rt△ABC中∠C=90°,AC=BC=4,将△ABC沿CB方向移动到△A1B1C1的位置,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E,∠ABC、∠BCD的角平分线交于点F.
如图,四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E,∠ABC、∠BCD的角平分线交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道.木板对地面的压强P(Pa)是木板面积S(m2)的反比例函数,其图象如下图所示.
某校科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道.木板对地面的压强P(Pa)是木板面积S(m2)的反比例函数,其图象如下图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com