Question

（2013四川南充，21，8分）如图，二次函数y=x²+bx－3b+3的图象与x轴交于A、B两点（点A在点B的左边），交y轴于点C，且经过点（b－2，2b²－5b－1）.

（1）求这条抛物线的解析式；

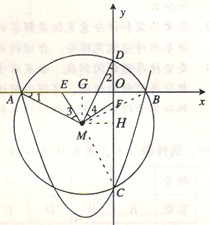
（2）⊙M过A、B、C三点，交y轴于另一点D，求点M的坐标；

（3）连接AM、DM，将∠AMD绕点M顺时针旋转，两边MA、MD与x轴、y轴分别交于点E、F，若△DMF为等腰三角形，求点E的坐标.

Answer 1

解：（1）把点（b－2，2b²－5b－1）代入解析式，得

2b²－5b－1=（b－2）²+b（b－2）－3b+3，              ……………1′

解得b=2.

∴抛物线的解析式为y=x²+2x－3.                       ……………2′

（2）由x²+2x－3=0，得x=－3或x=1.

∴A（－3，0）、B（1，0）、C（0，－3）.

抛物线的对称轴是直线x=－1，圆心M在直线x=－1上.      ……………3′

∴设M（－1，n），作MG⊥x轴于G，MH⊥y轴于H，连接MC、MB.

∴MH=1，BG=2.                                        ……………4′

∵MB=MC，∴BG²+MG²=MH²+CH²，

即4+n²=1+（3+n）²，解得n=－1，∴点M（－1，－1）     ……………5′

（3）如图，由M（－1，－1），得MG=MH.

∵MA=MD，∴Rt△AMG≌RtDMH，∴∠1=∠2.

由旋转可知∠3=∠4. ∴△AME≌△DMF.

若△DMF为等腰三角形，则△AME为等腰三角形.           ……………6′

设E（x，0），△AME为等腰三角形，分三种情况：

①AE=AM=，则x=－3，∴E（－3，0）；

②∵M在AB的垂直平分线上，

∴MA=ME=MB，∴E（1，0）                             ……………7′

③点E在AM的垂直平分线上，则AE=ME.

AE=x+3，ME²=MG²+EG²=1+（－1－x）²，∴（x+3）²=1+（－1－x）²，解得x=，∴E（，0）.

∴所求点E的坐标为（－3，0），（1，0），（，0）      ……………8′