
| A. | 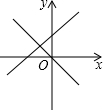 | B. |  | C. | 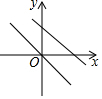 | D. | 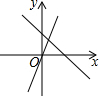 |
分析 根据“两数相乘,同号得正,异号得负”判断出a、b的符号,再根据一次函数的性质进行判断.
解答 解:①当-ab>0,正比例函数y=-abx过第一、三象限;
a与b异号,a>0,b<0时y=ax+b过第一、三、四象限,故B正确;
a<0,b>0时过第一、二、四象限,故D正确;
②当-ab<0时,正比例函数y=abx过第二、四象限;
a与b同号,同正时,y=ax+b过第一、二、三象限,故A正确;
同负时过第二、三、四象限,故C错误;
故选C.
点评 主要考查了一次函数的图象性质,要掌握它的性质才能灵活解题.
对于一次函数y=kx+b(k≠0,b≠0)的图象有四种情况:
①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限;
②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限;
③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限;
④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象限.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在4×4正方形网格中,黑色部分的 图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是( )
如图,在4×4正方形网格中,黑色部分的 图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是( )| A. | $\frac{3}{13}$ | B. | $\frac{4}{13}$ | C. | $\frac{5}{13}$ | D. | $\frac{6}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
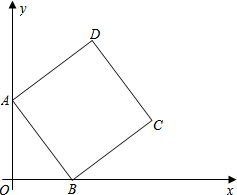 如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA、OB的长满足(x-$\frac{7}{2}$)2=$\frac{1}{4}$中的x.其中OA>OB.
如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA、OB的长满足(x-$\frac{7}{2}$)2=$\frac{1}{4}$中的x.其中OA>OB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC是直角三角形,∠ACB=90°,∠B=30°,以点C为旋转中心,将△ABC旋转到△A′B′C′的位置,且使A′B′经过点A.
如图,△ABC是直角三角形,∠ACB=90°,∠B=30°,以点C为旋转中心,将△ABC旋转到△A′B′C′的位置,且使A′B′经过点A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com