
试用字母说明:“ 一个两位数的十位数字与个位数字交换位置后,所得的新数与原数的差一定能被9整除”。
科目:初中数学 来源: 题型:
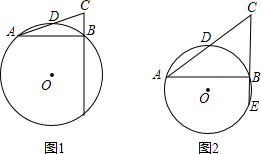 与线段CE相等,请说明理由;
与线段CE相等,请说明理由;| CF | CD |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |
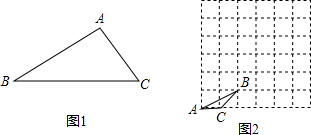 线交点处的三角形叫做格点三角形.友情提示:请在画出的三角形的项点处标上相对应的字母!)
线交点处的三角形叫做格点三角形.友情提示:请在画出的三角形的项点处标上相对应的字母!)查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 星期日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | g | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
| a | b | c |
| d | e | f |
| g | h | i |
查看答案和解析>>
科目:初中数学 来源:2006年初中毕业升学考试(江苏无锡卷)数学(带解析) 题型:解答题
(1)如图1,己知△ABC中,AB>AC。试用直尺(不带刻度)和圆规在图l中过点A作一条直线l,使点C关于直线l的对称点在边AB上(不要求写作法,也不必说明理由,但要保留作图痕迹)。
(2)如图2,己知格点△ABC,请在图2中分别画出与△ABC相似的格点△A1B1C1和格点△A2B2C2,并使△AlBlCl与△ABC的相似比等于2,而A2B2C2与△ABC的相似比等于 。(说明:顶点都在网格线交点处的三角形叫做格点三角形。友情提示:请在画出的三角形的项点处标上相对应的字母!)
。(说明:顶点都在网格线交点处的三角形叫做格点三角形。友情提示:请在画出的三角形的项点处标上相对应的字母!)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com