(2012•北京)在平面直角坐标系xOy中,对于任意两点P
1(x
1,y
1)与P
2(x
2,y
2)的“非常距离”,给出如下定义:
若|x
1-x
2|≥|y
1-y
2|,则点P
1与点P
2的“非常距离”为|x
1-x
2|;
若|x
1-x
2|<|y
1-y
2|,则点P
1与点P
2的“非常距离”为|y
1-y
2|.
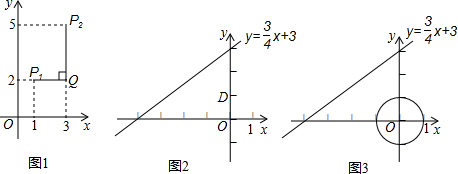
例如:点P
1(1,2),点P
2(3,5),因为|1-3|<|2-5|,所以点P
1与点P
2的“非常距离”为|2-5|=3,也就是图1中线段P
1Q与线段P
2Q长度的较大值(点Q为垂直于y轴的直线P
1Q与垂直于x轴的直线P
2Q交点).
(1)已知点A(-
,0),B为y轴上的一个动点,
①若点A与点B的“非常距离”为2,写出一个满足条件的点B的坐标;
②直接写出点A与点B的“非常距离”的最小值;
(2)已知C是直线y=
x+3上的一个动点,
①如图2,点D的坐标是(0,1),求点C与点D的“非常距离”的最小值及相应的点C的坐标;
②如图3,E是以原点O为圆心,1为半径的圆上的一个动点,求点C与点E的“非常距离”的最小值及相应的点E与点C的坐标.



 轻松暑假总复习系列答案
轻松暑假总复习系列答案