
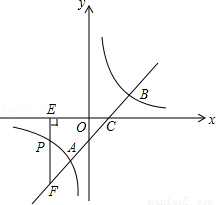
如图,直线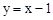 与反比例函数
与反比例函数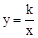 的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(-1,m).
的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(-1,m).
(1)求反比例函数的解析式;
(2)若点P(n,1)是反比例函数图象上一点,过点P作PE⊥x轴于点E,延长EP交直线AB于点F,求△CEF的面积.
解:(1)将点A的坐标代入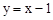 ,可得:
,可得: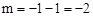 。∴点A的坐标为(-1,-2)。
。∴点A的坐标为(-1,-2)。
将点A(-1,-2)代入反比例函数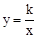 ,可得:
,可得: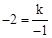 ,
,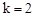 。
。
∴反比例函数解析式为: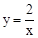 。
。
(2)将点P的纵坐标y=-1,代入反比例函数关系式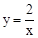 可得:x=-2,
可得:x=-2,
∴点P的坐标为(-2,-1)
将点F的横坐标x=-2代入直线解析式可得:y=-3,∴点F的坐标为(-2,-3)。
∴EF=3,CE=OE+OC=2+1=3,∴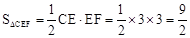 。
。
【解析】(1)将点A的坐标代入直线解析式求出m的值,再将点A的坐标代入反比例函数解析式可求出k的值,继而得出反比例函数关系式。
(2)将点P的纵坐标代入反比例函数解析式可求出点P的横坐标,将点P的横坐标和点F的横坐标相等,将点F的横坐标代入直线解析式可求出点F的纵坐标,将点的坐标转换为线段的长度后,即可计算△CEF的面积。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 直线y=kx+b与反比例函数y=
直线y=kx+b与反比例函数y=| m | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
直线![]() 与反比例函数
与反比例函数![]() 的图象相交于点
的图象相交于点![]() 、
、![]() ,
,
 与
与![]() 轴交于点
轴交于点![]() ,其中点
,其中点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() .
.
(1)试确定反比例函数的关系式.
(2)求![]() 的面积.
的面积.
(3)如图直接写出反比例函数值大于一次函数值的自变量![]() 的取值范围.
的取值范围.
|
查看答案和解析>>
科目:初中数学 来源: 题型:
直线 与反比例函数
与反比例函数![]() 的图象相交于点
的图象相交于点![]() 、
、![]() ,
,
与 轴交于点
轴交于点![]() ,其中点
,其中点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的横坐标为
的横坐标为![]()
1.试确定反比例函数的关系式.
2.求![]() 的面积
的面积
3.如图直接写出反比例函数值大于一次函数值的自变量![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源:《第22章 二次函数》2012年单元测试卷A(亳州市风华中学)(解析版) 题型:解答题
 (x<0)的图象相交于点A、B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4.
(x<0)的图象相交于点A、B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4.
查看答案和解析>>
科目:初中数学 来源:2012届重庆一中九年级上学期开学考试数学卷 题型:填空题
直线 与反比例函数
与反比例函数 的图象相交于点
的图象相交于点 、
、 ,
,
 与
与 轴交于点
轴交于点 ,其中点
,其中点 的坐标为
的坐标为 ,点
,点 的横坐标为
的横坐标为 .
.
(1)试确定反比例函数的关系式.
(2)求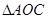 的面积.
的面积.
(3)如图直接写出反比例函数值大于一次函数值的自变量 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com