
 .将△ABO绕坐标原点O顺时针旋
.将△ABO绕坐标原点O顺时针旋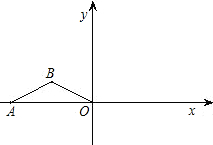 转90°,得到△A1B1O,再继续旋转90°,得到△A2B2O.抛物线y=ax2+bx+3经过B、B1两点.
转90°,得到△A1B1O,再继续旋转90°,得到△A2B2O.抛物线y=ax2+bx+3经过B、B1两点.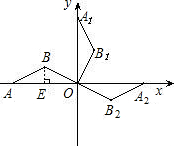 解:
解: OA=2.
OA=2. ,
,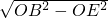 =1.
=1.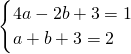 .
.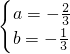 .
. x2-
x2- x+3.
x+3. ×22-
×22- ×2+3=-
×2+3=- ≠-1,
≠-1, x2-
x2- x+3的交点,
x+3的交点,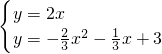 .
. ,
,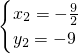 .
. ,-9).
,-9). ,
, )(
)( ,
, ).
).

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
| 5 |
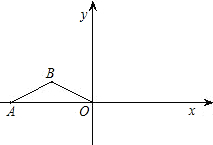 转90°,得到△A1B1O,再继续旋转90°,得到△A2B2O.抛物线y=ax2+bx+3经过B、B1两点.
转90°,得到△A1B1O,再继续旋转90°,得到△A2B2O.抛物线y=ax2+bx+3经过B、B1两点.查看答案和解析>>
科目:初中数学 来源: 题型:
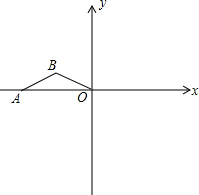 如图,点A在x轴的负半轴上,OA=4,AB=OB=
如图,点A在x轴的负半轴上,OA=4,AB=OB=| 5 |
| 9 |
| 2 |
| 9 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
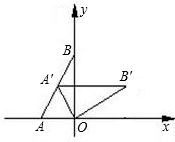 如图,点A在x轴的负半轴上,点B在y轴的正半轴上,∠ABO=30°,AO=2,将△AOB绕原点O顺时针旋转后得到△A′OB′.当点A′恰好落在AB上时,点B′的坐标为
如图,点A在x轴的负半轴上,点B在y轴的正半轴上,∠ABO=30°,AO=2,将△AOB绕原点O顺时针旋转后得到△A′OB′.当点A′恰好落在AB上时,点B′的坐标为查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,点B在y轴的负半轴上,点A在x轴的正半轴上,且OA=2,tan∠OAB=2.
已知:如图,点B在y轴的负半轴上,点A在x轴的正半轴上,且OA=2,tan∠OAB=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
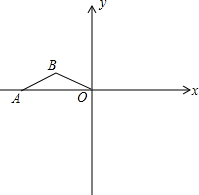 如图,点A在x轴的负半轴上,OA=4,AB=OB=
如图,点A在x轴的负半轴上,OA=4,AB=OB= ,将△ABO绕坐标原点O顺时针旋转90°,得到△A1B1O,再继续旋转90°,得到△A2B2O,抛物线y=ax2+bx+3经过B、B1两点.
,将△ABO绕坐标原点O顺时针旋转90°,得到△A1B1O,再继续旋转90°,得到△A2B2O,抛物线y=ax2+bx+3经过B、B1两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com