
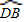 上有一动点M,连接PM,AM.
上有一动点M,连接PM,AM.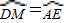 ,弦ED=3cm,⊙O的半径为2cm.则cos∠MAB=______.
,弦ED=3cm,⊙O的半径为2cm.则cos∠MAB=______.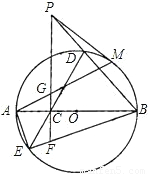
 ,代入数据可得答案;
,代入数据可得答案; ,进而可得答案;
,进而可得答案; (1)解:90°;直径所对的圆周角是直角;
(1)解:90°;直径所对的圆周角是直角; (3分)
(3分)


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源:2006年全国中考数学试题汇编《二次函数》(09)(解析版) 题型:解答题
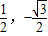 ),过A点作x轴的平行线l,在l上有一不与A点重合的点B,连接OA,OB.将OA绕O点顺时针方向旋转α°到OA1,OB绕O点逆时针方向旋转α°到OB1.
),过A点作x轴的平行线l,在l上有一不与A点重合的点B,连接OA,OB.将OA绕O点顺时针方向旋转α°到OA1,OB绕O点逆时针方向旋转α°到OB1.
查看答案和解析>>
科目:初中数学 来源:2006年湖北省荆州市中考数学试卷(解析版) 题型:解答题
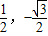 ),过A点作x轴的平行线l,在l上有一不与A点重合的点B,连接OA,OB.将OA绕O点顺时针方向旋转α°到OA1,OB绕O点逆时针方向旋转α°到OB1.
),过A点作x轴的平行线l,在l上有一不与A点重合的点B,连接OA,OB.将OA绕O点顺时针方向旋转α°到OA1,OB绕O点逆时针方向旋转α°到OB1.
查看答案和解析>>
科目:初中数学 来源:2011年中考复习专项训练《实验与操作》(解析版) 题型:选择题
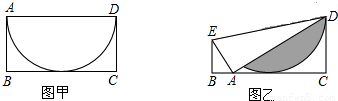
 )cm2
)cm2 π+
π+ )cm2
)cm2 π-
π- )cm2
)cm2 π+
π+ )cm2
)cm2查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com