
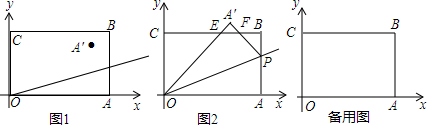
���� ��1����ͼ1������OA�䣬AA�䣮��A�䣨x��3�������ݾ��ε����ʣ����������ͼ�ε������Լ����ɶ������CA��=4��Ȼ����A��5��0�����AA����е�D�������ǣ�4.5��1.5�����Ӷ����k��ֵ��
��2�����ݵȱ������ε��ж��ó���A'OA�ǵȱ������Σ��ٵó������߽���ʽ���ɣ�
��3������ȫ�������εĶ�Ӧ����ȺͶ�Ӧ����ȡ����ɶ����Լ����к����Ķ�������k��ֵ��
��4���������⣬����ͼ�Σ�����ͼ�λش����⣮
��� �⣺��1������A��ǡ����CB����ʱ������A��O��A��P����ͼ1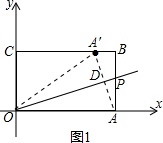
��OA��=OA=5��OC=3��
��CA��=$\sqrt{OA{��}^{2}-O{C}^{2}}$=$\sqrt{52-32}$=4
��A��B=CB-CA��=5-4=1��
��PA=x����A��P=PA=x��BP=3-x
��Rt��A��PB��A��B2+BP2=A��P2
��12+��3-x��2=x2�����x=$\frac{5}{3}$��
��P��5��$\frac{5}{3}$����
���k=$\frac{1}{3}$��
��2������A'O��A'P��A'A����A'A������OP�ڵ�D����ͼ2��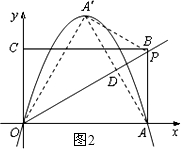
��OP��ֱƽ��A'A��
�߾���O��A��A'�����������ǡ����A��Ϊ���㣬
���������ߵĶԳ��Կ�֪A'O=A'A=2A'D��
���A'OD=30�㣬
���AOD=��A'OD=30�㣬
��PA=$\frac{\sqrt{3}}{3}OA=60��$��
���A'OA�ǵȱ������Σ�
���A'������Ϊ$��\frac{5}{2}��\frac{5\sqrt{3}}{2}��$��
�������ߵĽ���ʽΪ$y=a��x-\frac{5}{2}��^{2}+\frac{5\sqrt{3}}{2}$��
��O��0��0��������ʽ����$0=a��0-\frac{5}{2}��^{2}+\frac{5\sqrt{3}}{2}$��
��ã�a=-$\frac{2\sqrt{3}}{5}$��
�������ߵĽ���ʽΪ$-\frac{2\sqrt{3}}{5}��x-\frac{5}{2}��^{2}+\frac{5\sqrt{3}}{2}$��
��3���������ʵ��k��ʹ��A��EF�ա�BPF����ͼ3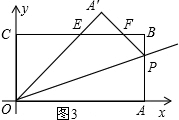
�ߡ�A��=��B=90�㣬��A��FE=��BFP
��A��E=BP��A��F=BF
��A��E=BP=a��A��F=BF=b
��A��P=PA=3-a��EF=PF=3-a-b��OE=5-a
CE=5-��3-a-b��-b=2+a
��Rt��OCE��OC2+CE2=OE2
��32+��2+a��2=��5-a��2�����a=$\frac{6}{7}$
��PA=3-$\frac{6}{7}$=$\frac{15}{7}$��
��P��5��$\frac{15}{7}$��
��k=$\frac{3}{7}$��
��4������P��BC����ʱ����M�����OABC��6�����㣻
�ٵ���M��BC�����ڵ�Dʱ��
��MD��BC��
��DE��AB��OC��
��DE=OC=3��
��M��OP���е㣬
��E��OA���е㣬
��ME=$\frac{1}{2}$PA��
��PAΪx����ME=$\frac{1}{2}x$��DM=$\frac{1}{2}OP=\frac{1}{2}\sqrt{{x}^{2}+{5}^{2}}$��
��DM+ME=DE��
��$\frac{1}{2}\sqrt{{x}^{2}+{5}^{2}}+\frac{1}{2}x=3$��
��ã�x=$\frac{11}{12}$��
��P��5��$\frac{11}{12}$����
��k=$\frac{11}{60}$��
�ڵ���M��AB�����ڵ�Eʱ��
��CPΪx����DM=$\frac{1}{2}x$��ME=$\frac{1}{2}OP=\frac{1}{2}\sqrt{{x}^{2}+{3}^{2}}$��
��DM+ME=DE��
��$\frac{1}{2}x+\frac{1}{2}\sqrt{{x}^{2}+{3}^{2}}=5$��
��ã�x=$\frac{91}{20}$��
��P��$\frac{91}{20}$��3����
��k=$\frac{60}{91}$��
�֡ߵ���P���B�غ�ʱ����M����O��A��B��C�ĵ㣬��ʱk=$\frac{3}{5}$��
�ʿɵã���ͼ4��
��0��k��$\frac{11}{60}$ʱ����4����ͬ�㣬
k=$\frac{11}{60}$��$\frac{60}{91}$ʱ����5����ͬ�㣬
k=$\frac{3}{5}$ʱ����4����ͬ�㣬
�������6�����㣬k��ȡֵ��Χ�ǣ�$\frac{11}{60}$��k��$\frac{60}{91}$��k��$\frac{3}{5}$��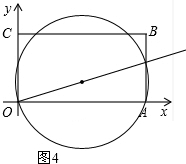
�ʴ�Ϊ��6��
���� ���⿼���˶��κ����ۺ����Լ�ȫ�������ε����ʺ�Բ���ۺϵ�֪ʶ����������λ�����k��ȡֵ��Χ�����ó��𰸣�


 �¿α�ͬ��ѵ��ϵ�д�
�¿α�ͬ��ѵ��ϵ�д� һ����ʦ����Ӧ����������һ��ȫϵ�д�
һ����ʦ����Ӧ����������һ��ȫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
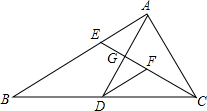 ��ͼ���ڡ�ABC�У�AD��BC���ϵ����ߣ���E�ڱ�AB�ϣ�CE��AD���ڵ�G����F��CE���е㣬��G��EF���е㣮��֤��AE=$\frac{1}{2}$BE��
��ͼ���ڡ�ABC�У�AD��BC���ϵ����ߣ���E�ڱ�AB�ϣ�CE��AD���ڵ�G����F��CE���е㣬��G��EF���е㣮��֤��AE=$\frac{1}{2}$BE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��60Ԫ���ۼ�ƫ�Ԫ�� | -15 | -12 | -8 | 0 | +4 | +5 | +7 |
| ���������� | 1 | 3 | 5 | 4 | 4 | 2 | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��c=0ʱ��������ͼ��ԭ�� | |
| B�� | ��b=0ʱ��������ͼ�����y��Գ� | |
| C�� | ��������ͼ�����A��1��2����B��7��2���������ĶԳ���Ϊֱ��x=3 | |
| D�� | ��c��0�Һ�����ͼ������ʱ������ax2+bx+c=0������������ȵ�ʵ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
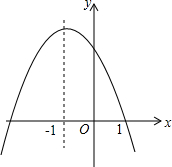 ���κ���y=ax2+bx+c��a��0���IJ���ͼ����ͼ��ʾ���������½��ۣ���a+b+c��0����c-a��0����a-2b+4c��0����m��am+b��+b��a��m��-1����������ȷ�Ľ��۵ĸ����ǣ�������
���κ���y=ax2+bx+c��a��0���IJ���ͼ����ͼ��ʾ���������½��ۣ���a+b+c��0����c-a��0����a-2b+4c��0����m��am+b��+b��a��m��-1����������ȷ�Ľ��۵ĸ����ǣ�������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com