Question

已知抛物线y=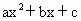开口向下，并且经过A(0，1)和M(2，－3)两点．

(1)若抛物线的对称轴为直线x=－1，求此抛物线的解析式．

(2)如果抛物线的对称轴在y轴的左侧，试求a的取值范围．

(3)如果抛物线与x轴交于B、C两点，且∠BAC=90°，求此时a的值．

Answer 1

答案：略
解析：

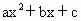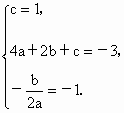
解：(1)因为抛物线y=经过A(0，1)和M(2，－3)两点，且对称轴为直线x=－1，于是，有 解这个方程组，得a=－，b=－1，c=1． 所以，抛物线解析式． (2)由题意得 消去c，得b=－2a－2． 又∵抛物线开口向下，对称轴在y轴左侧， ∴ ∴b＜0． ∴b=－2a－2＜0， ∴解得a＞－1． ∴a的取值范围是－1＜a＜0． (3)由抛物线开口向下，且经过点A(0，1)知：它与x轴的两个交点B、C分别在原点的两旁，此时B、C两点的横坐标异号(如图所示)，OA=c=1． 又∵∠BAC=90°，∴点A必在以BC为直径的圆上． 又∵OA⊥BC于O，∴=OB·OC． ∵b=－2a－2，c=1，∴抛物线方程变为． 设此抛物线与x轴的两个交点分别为B(，0)，C(，0)，则，是方程的两根， ∴·=，∴OB·OC=||·||=|·|=－·，(·＜0)，∴OB·OC=－． 又∵=OB·OC=1，∴1=－，解得a=－1． 经检验，当a=－1时，所确定的抛物线符合题意，∴a的值为－1．