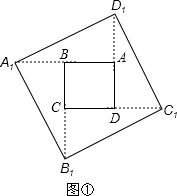
解:(1)如图①所示.
(2)设正方形ABCD的边长为a,
则AA
1=2a,S
△AA1D1=

•AA
1•AD
1=a
2,
同理,S
△BB1A1=S
△CC1B1=S
△DD1C1=a
2,
∴S
1=S
△AA1D1+S
△BB1A1+S
△CC1B1+S
△DD1C1+S
正方形ABCD=5a
2=5S.
(本问也可以先证明四边形A
1B
1C
1D
1是正方形,再求出其边长为

a,从而算出S
四边形A1B1C1D1=5S)
(3)S
1=S
2理由如下:
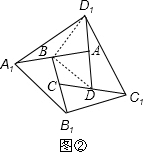
首先画出图形②,连接BD、BD
1,
∵△BDD
1中,AB是中线,
∴S
△ABD1=S
△ABD.
又∵△AA
1D
1中,BD
1是中线,
∴S
△ABD1=S
△A1BD1∴S
△AA1D1=2S
△ABD同理,得S
△CC1B1=2S
△CBD∴S
△AA1D1+S
△CC1B1=2(S
△ABD+S
△CBD)=2S.
同理,得S
△BA1B1+S
△DD1C1=2S,
∴S
2=S
△AA1D1+S
△BB1A1+S
△CC1B1+S
△DD1C1+S
四边形ABCD=5S.
由(2)得,S
1=5S.
∴S
1=S
2.
分析:(1)根据对称的性质可知.使得点A
1和点A关于点B对称,即是连接AB并延长相同的长度找到对应点A′,其它三点同样的方法找到对应点,顺次连接.
(2)设正方形ABCD的边长为a,根据两个正方形边长的比值,利用面积比等于相似比,来求小正方形的面积.
(3)相等.因为一个四边形可以分成两个三角形,根据三角形的面积公式,等底等高的三角形面积相等.
点评:本题是一道综合性很强的题,综合了轴对称,正方形的面积,及四边形,三角形的面积,所以我们学生学知识一定不要机械的学,要会联系起来.

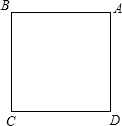 如图,已知正方形ABCD的面积为S.
如图,已知正方形ABCD的面积为S. •AA1•AD1=a2,
•AA1•AD1=a2,
 a,从而算出S四边形A1B1C1D1=5S)
a,从而算出S四边形A1B1C1D1=5S)


 (2013•北碚区模拟)如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.
(2013•北碚区模拟)如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点. 如图,已知正方形ABCD,点E在BC边上,将△DCE绕某点G旋转得到△CBF,点F恰好在AB边上.
如图,已知正方形ABCD,点E在BC边上,将△DCE绕某点G旋转得到△CBF,点F恰好在AB边上. 如图,已知正方形ABCD的对角线AC,BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.
如图,已知正方形ABCD的对角线AC,BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.