练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．如图，点A，B，C，D，E为⊙O的五等分点，动点M从圆心O出发，沿线段OA→劣弧AC→线段CO的路线做匀速运动，设运动的时间为t，∠DME的度数为y，则下列图象中表示y与t之间函数关系最恰当的是（　　）
    A．B．C．D．

    分析 根据题意，分M在OA、$\widehat{AC}$、CO之间3个阶段，分别分析变化的趋势，又由点P作匀速运动，故①③都是线段，分析选项可得答案．

    解答 解：根据题意，分3个阶段；
    ①P在OA之间，∠DME逐渐减小，到A点时，为36°，
    ②P在$\widehat{AC}$之间，∠DME保持36°，大小不变，
    ③P在CO之间，∠DME逐渐增大，到O点时，为72°；
    又由点P作匀速运动，故①③都是线段；
    分析可得：B符合3个阶段的描述；
    故选B．

    点评 本题主要考查了函数图象与几何变换，解决此类问题，注意将过程分成几个阶段，依次分析各个阶段得变化情况，进而综合可得整体得变化情况．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．在平面直角坐标系中，O为坐标原点，点A的坐标为（2x+y-3，x-2y），它关于x轴的对称点A1的坐标为（x+3，y-4），关于y轴的对称点为A2．
    （1）求A1、A2的坐标；
    （2）证明：O为线段A1A2的中点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

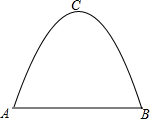    15．一条单车道的抛物线形隧道如图所示．隧道中公路的宽度AB=8m，隧道的最高点C到公路的距离为6m．
    （1）建立适当的平面直角坐标系，求抛物线的表达式；
    （2）现有一辆货车的高度是4.4m，货车的宽度是2m，为了保证安全，车顶距离隧道顶部至少0.5m，通过计算说明这辆货车能否安全通过这条隧道．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．已知直角三角形ABC中，斜边AB的长为m，∠B=50°，则直角边BC的长是（　　）
    A．msin50°B．mtan50°C．mcos50°D．$\frac{m}{{tan{{50}°}}}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．把所有正偶数从小到大排列，并按如下规律分组：（2），（4，6），（8，10，12），（14，16，18，20），…，现有等式Am=（i，j）表示正偶数m是第i组第j个数（从左往右数）．如A2=（1，1），A10=（3，2），A18=（4，3），则A2018可表示为（　　）
    A．（45，19）B．（45，20）C．（44，19）D．（44，20）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．下列各式中，是一元一次方程的是（　　）
    A．4x+3B．$\frac{1}{x}$=2C．2x+y=5D．3x=2x-1

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．已知二次函数y1=ax2+bx+c（a≠0）和一次函数y2=kx+n（k≠0）的图象如图所示，下面有四个推断：
    ①二次函数y1有最大值
    ②二次函数y1的图象关于直线x=-1对称
    ③当x=-2时，二次函数y1的值大于0
    ④过动点P（m，0）且垂直于x轴的直线与y1，y2的图象的交点分别为C，D，当点C位于点D上方时，m的取值范围是m＜-3或m＞-1．
    其中正确的是（　　）
    A．①③B．①④C．②③D．②④

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．抛物线y=-（x-2）2向右平移2个单位得到的抛物线的解析式为（　　）
    A．y=-x2B．y=-（x-4）2C．y=-（x-2）2+2D．y=-（x-2）2-2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．（1）先化简，再求值：2x2+y2+（2y2-3x2）-2（y2-2x2），其中x=1，y=2．
    （2）解方程：$\frac{x}{6}$-$\frac{30-x}{4}$=5．

    查看答案和解析>>

    同步练习册答案