
分析 (1)利用立方根的定义得到x+3=-3,然后解一元一次方程即可;
(2)先变形得到(x-1)2=$\frac{25}{16}$,则利用平方根的定义得到x-1=±$\frac{5}{4}$,然后解两个一元一次方程即可.
解答 解:(1)x+3=-3,
所以x=-6;
(2)(x-1)2=$\frac{25}{16}$,
x-1=±$\frac{5}{4}$,
所以x=$\frac{9}{4}$或x=-$\frac{1}{4}$.
点评 本题考查了立方根:如果一个数的立方等于a,那么这个数叫做a的立方根或三次方根.这就是说,如果x3=a,那么x叫做a的立方根.记作:$\root{3}{a}$.也考查了平方根.


科目:初中数学 来源: 题型:选择题
 二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法中错误的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法中错误的是( )| A. | 函数有最小值 | B. | 对称轴是直线x=$\frac{1}{2}$ | ||
| C. | 当x=-1或x=2时,y=0 | D. | 当x>0时,y随x的增大而减小 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
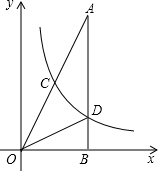 如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y=$\frac{k}{x}$在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.
如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y=$\frac{k}{x}$在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
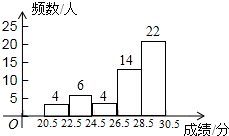 九年级(3)班共有50名同学,如图是该班一次体育模拟测试成绩的频数分布直方图(满分为30分,成绩均为整数).若将不低于23分的成绩评为合格,则该班此次成绩达到合格的同学占全班人数的百分比是( )
九年级(3)班共有50名同学,如图是该班一次体育模拟测试成绩的频数分布直方图(满分为30分,成绩均为整数).若将不低于23分的成绩评为合格,则该班此次成绩达到合格的同学占全班人数的百分比是( )| A. | 80% | B. | 70% | C. | 92% | D. | 86% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com