
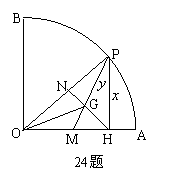
如图, 在半径为6,圆心角为90°的扇形OAB的弧AB上, 有一个动点P, PH⊥OA,垂足为H, △PHO的中线PM与NH交于点G.
有一个动点P, PH⊥OA,垂足为H, △PHO的中线PM与NH交于点G.
(1)求证: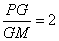 ;
;
(2)设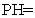
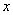 ,
, 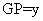 ,求
,求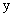 关于
关于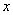 的函数解析式,并写自变量
的函数解析式,并写自变量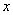 的取值范围;
的取值范围;
(3)如果△PGH是等腰三角形,试求出线段PH的长.
(1)连接MN
∵NH、PM是三角形的中线………………………………………1分
∴△OMN∽△OHP,MN=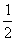 PH………………………………………2分
PH………………………………………2分
∴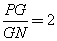 ……………………………………………………………………………………3分
……………………………………………………………………………………3分
(2)在Rt△O PH中,
PH中,
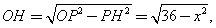
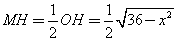 …………………………………………………………………5分
…………………………………………………………………5分
 在Rt△MPH中,
在Rt△MPH中,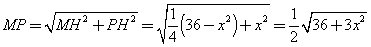 ……………6分
……………6分
∴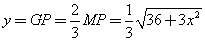
 (0<
(0<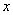 <6)…………………………………………8分
<6)…………………………………………8分
(3)△PGH是等腰三角形有三种可能情况:
①GP=PH,即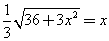 ,解得
,解得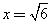 ,……………………………………………9分
,……………………………………………9分
②PH=GH,即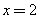 ,…………………………………………………………………………10分
,…………………………………………………………………………10分
③GP=GH,即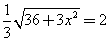 ,解得
,解得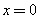 …………
………… ……………………………………11分
……………………………………11分
综上所述,如果△PGH是等腰三角形,那么线段PH的长等于PH=GH,即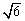 或
或
2。


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
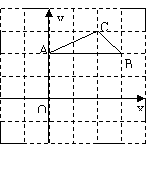
如图,在平面直角坐标系中,点A,B,C的坐标分别为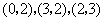 .
.
(1)请在图中画出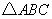 向下平移3个单位的像
向下平移3个单位的像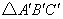 ;(2)若一个二次函数的图象经过(1)中
;(2)若一个二次函数的图象经过(1)中 的三个顶点
的三个顶点 ,求此二次函数的关系式.
,求此二次函数的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
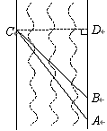
在一次数学活动课上,某校初三数学老师带领学生去测河宽,如图13所示,某学生在河东岸点 处观测到河对岸水边有一点
处观测到河对岸水边有一点 ,测得
,测得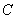 在
在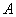 北偏西
北偏西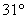 的方向上,沿河岸向北前行20米到达
的方向上,沿河岸向北前行20米到达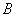 处,测得
处,测得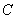 在
在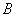 北偏西
北偏西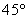 的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.(参考数值:tan31°≈
的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.(参考数值:tan31°≈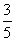 ,sin31°≈
,sin31°≈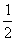 )
) 
查看答案和解析>>
科目:初中数学 来源: 题型:
在下列条件中:①∠A+∠B=∠C;②∠A:∠B∠:∠C=1:2:3;③∠A=90°-∠B;④∠A=∠B=∠C,能确定△ABC是直角三角形的条件有( )个.
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com