
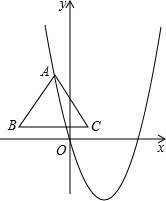
 如图,已知抛物线
如图,已知抛物线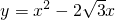 ,等边△ABC的边长为
,等边△ABC的边长为 ,顶点A在抛物线上滑动,且BC边始终平行水平方向,当△ABC在滑动过程中,点B落在坐标轴上时,C点坐标是:________.
,顶点A在抛物线上滑动,且BC边始终平行水平方向,当△ABC在滑动过程中,点B落在坐标轴上时,C点坐标是:________. -
- ,0),(2
,0),(2 +
+ ,0),(2
,0),(2 ,-6)
,-6) ,然后代入抛物线解析式求出点A的纵坐标,再向下3个单位长度即为点C的纵坐标,点C的横坐标的长度等于等边三角形的边长,写出即可.
,然后代入抛物线解析式求出点A的纵坐标,再向下3个单位长度即为点C的纵坐标,点C的横坐标的长度等于等边三角形的边长,写出即可.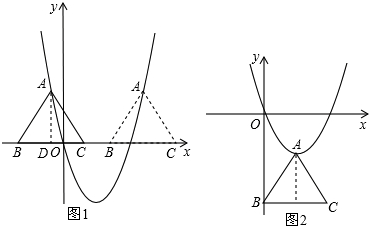 解:∵等边△ABC的边长为
解:∵等边△ABC的边长为 ,
, ×
× =3,边长的一半为
=3,边长的一半为 ,
, x=3,
x=3, x-3=0,
x-3=0, =
=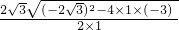 =
= ±
± ,
, -
- 时,
时, -
- +
+ =2
=2 -
- ,
, -
- ,0),
,0), +
+ 时,
时, +
+ +
+ =2
=2 +
+ ,
, +
+ ,0);
,0); ,
, 2-2
2-2 ×
× =3-6=-3,
=3-6=-3, ,-6),
,-6), -
- ,0),(2
,0),(2 +
+ ,0),(2
,0),(2 ,-6).
,-6). -
- ,0),(2
,0),(2 +
+ ,0),(2
,0),(2 ,-6).
,-6).

科目:初中数学 来源: 题型:
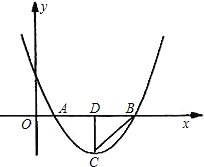 对称轴与x轴的交点.
对称轴与x轴的交点.| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 4 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知抛物线C1的顶点坐标是D(1,4),且经过点C(2,3),又与x轴交于点A、E(点A在点E左边),与y轴交于点B.
如图,已知抛物线C1的顶点坐标是D(1,4),且经过点C(2,3),又与x轴交于点A、E(点A在点E左边),与y轴交于点B.查看答案和解析>>
科目:初中数学 来源:2011年浙江省绍兴市绍兴县成章中学中考数学一模试卷(解析版) 题型:填空题
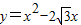 ,等边△ABC的边长为
,等边△ABC的边长为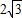 ,顶点A在抛物线上滑动,且BC边始终平行水平方向,当△ABC在滑动过程中,点B落在坐标轴上时,C点坐标是: .
,顶点A在抛物线上滑动,且BC边始终平行水平方向,当△ABC在滑动过程中,点B落在坐标轴上时,C点坐标是: .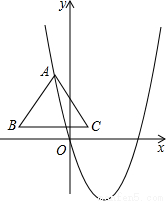
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com