练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．甲乙两人从相距1500米的A、B两地同时出发相向而行，甲骑自行车，速度是7.5米/秒，乙步行，速度是2.5米/秒，甲出发1分钟后忘记带东西，迅速返回去取（掉头时间及取东西时间不计），则在乙出发250或230秒后，两人相距100米．

    分析 由题意可知：甲出发1分钟后忘记带东西，迅速返回去取，相当于乙提前2分钟，由此分两种情况探讨：①甲、乙相遇前相距100米；②甲、乙相遇后相距100米；由此设出未知数，列出方程解答即可．

    解答 解：乙出发x秒后，两人相距100米．由题意得
    ①甲、乙相遇前相距100米；
    2.5x+7.5（x-120）=1500-100
    解得：x=230
    ②甲、乙相遇后相距100米；
    7.5（x-120）+2.5x=1500+100
    解得x=250
    答：则在乙出发230或250秒后，两人相距100米．
    故答案为：230或250．

    点评 此题考查一元一次方程的实际运用，掌握行程问题中的相遇问题的基本数量关系是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    11．化简：（am）2•（a3）n-（am-1）2•a2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

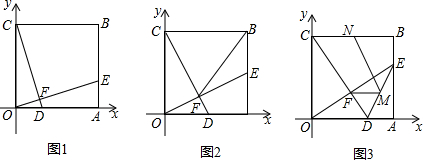    13．如图1，在平面直角坐标系中，OABC是边长为1的正方形，E是AB上一动点，D是OA上一动点，且OD=AE，OE与CD交于点F．
    （1）求证：CD⊥OE；
    （2）如图2，当点E为AB的中点时，求BF的长；
    （3）如图3，设M、N分别为DE、BC的中点，当FM+MN的值最小时，求此时点E的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

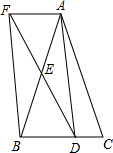    10．如图，在△ABC中，点D、E分别是BC、AB边的中点，过A点作AF∥BC交DE的延长线于F点，连接AD、BF．
    （1）求证：四边形ADBF是平行四边形；
    （2）当△ABC满足什么条件时，四边形ADBF是矩形？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．3$\sqrt{5}$+4$\sqrt{5}$-8$\sqrt{5}$=-$\sqrt{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．下列运算正确的是（　　）
    A．$\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$B．$\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$C．$\sqrt{{5}^{2}-{3}^{2}}$=5-3D．$\sqrt{8}$$÷\sqrt{2}$=4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．若关于x的分式方程$\frac{2x-a}{x+1}$=1的解为正数，求实数a的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．判断下列几组数据中，可以作为直角三角形的三条边的是（　　）
    A．2，3，4B．1，4，9C．1，$\frac{1}{2}$，$\frac{1}{3}$D．1，$\sqrt{2}$，$\sqrt{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．下列事件是必然事件的是（　　）
    A．抛一枚硬币反面朝上
    B．明天是晴天
    C．打开电视正在播放新闻
    D．袋中有两个黄球，任意摸出一球是黄球

    查看答案和解析>>

    同步练习册答案