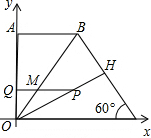
解:(1)∵AB∥OC
∴∠OAB=∠AOC=90°
在Rt△OAB中,AB=2,AO=2

∴OB=4,tan∠ABO=

,
∴∠ABO=60°,
∵AB∥OC
∴∠BOC=60°
又∵∠BCO=60°
∴△BOC为等边三角形
∴OH=OBcos30°=4×

=2

;
(2)∵OP=OH-PH=2

-t
∴x
p=OPcos30°=3-

t,
y
p=OPsin30°=

-

t.
∴S=

•OQ•x
p=

•t•(3-

t)
=
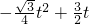
(o<t<2

)
即S=-
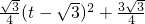
∴当t=

时,S
最大=

;
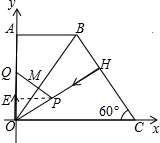
(3)①若△OPM为等腰三角形,则:
(i)若OM=PM,∠MPO=∠MOP=∠POC
∴PQ∥OC
∴OQ=y
p即t=

-

解得:t=

此时S=
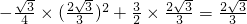
(ii)若OP=OM,∠OPM=∠OMP=75°,∴∠OQP=45°
过P点作PE⊥OA,垂足为E,则有:EQ=EP
即t-(

-

t)=3-

t
解得:t=2
此时S=
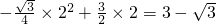
(iii)若OP=PM,∠POM=∠PMO=∠AOB,∴PQ∥OA
此时Q在AB上,不满足题意.
②线段OM长的最大值为

.
分析:(1)由图知图形很特殊,利用直线的平行关系,求出直角,在直角三角形中解题,从而求出OH的长;
(2)由几何关系求出P点坐标,将△OPQ的面积为S用t来表示,转化为求函数最值问题;
(3)思维要严密,△OPM为等腰三角形时,要分三种情况来讨论;最后一问求出M点坐标,同样转化为函数最值问题.
点评:此题是一道动态型压轴题,融函数、数形结合,分类讨论等重要数学思想于其中的综合题,考查的知识主要有:直线形、解直角三角形、函数等重点知识,此题计算较易,但对学生的能力要求较高,解题时要切实把握几何图形的运动过程,用运动、发展、全面的观点分析图形,采取“动中求静,静中求动”的解题策略,才能作出正确的解答.该题综合性强、灵活性大、区分度高,是今后中考命题的抢眼题型,要引起我们今后教学的高度关注.

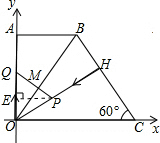
 ),∠BCO=60°,OH⊥BC于点H.动点P从点H出发,沿线段HO向点O运动,
),∠BCO=60°,OH⊥BC于点H.动点P从点H出发,沿线段HO向点O运动,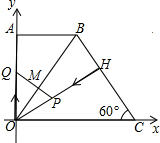 动点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度.设点P运动的时间为t秒.
动点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度.设点P运动的时间为t秒. 解:(1)∵AB∥OC
解:(1)∵AB∥OC
 ,
, =2
=2 ;
; -t
-t t,
t, -
- t.
t. •OQ•xp=
•OQ•xp= •t•(3-
•t•(3- t)
t)
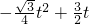 (o<t<2
(o<t<2 )
)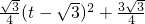
 时,S最大=
时,S最大= ;
; -
-

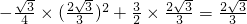
 -
- t)=3-
t)=3- t
t
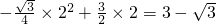
 .
.


 如图,直角梯形OABF中,∠OAB=∠B=90°,A点在x轴上,双曲线y=
如图,直角梯形OABF中,∠OAB=∠B=90°,A点在x轴上,双曲线y=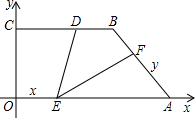 是BC上一点,BD=
是BC上一点,BD=