
分析 (1)将x=-2代入计算,函数值为0即可.
(2)分两种情形讨论:①若k=0,此函数为一次函数y=-x-2,②若k≠0,根据二次函数的性质即可解决问题.
(3)分两种情形讨论:①若k=0,不存在,②k≠O,列出方程即可解决.
解答 解:(1)将x=-2代入,得y=k(-2)2+(2k-1)•(-2)-2=0,
故不论k取何值,此函数图象一定经过点(-2,0).
(2)①若k=0,此函数为一次函数y=-x-2,当x>0时,y随x的增大而减小,
∴k=0符合题意.
②若k≠0,此函数为二次函数,而图象一定经过(-2,0)、(0,-2)
∴要使当x>0时,y随x的增大而减小,开口向下,须满足k<0即可.
综上,k的取值范围是k≤0.
(3)若k=0,此函数为一次函数y=-x-2,
∵x的取值为全体实数,
∴y无最小值,
若k≠0,此函数为二次函数,若存在最小值为-3,
则$\frac{-8k-(2k-1)^{2}}{4k}$=-3,且k>0,
解得:k=$\frac{2±\sqrt{3}}{2}$ 符合题意,
∴当k=$\frac{2±\sqrt{3}}{2}$时,函数存在最小值-3.
点评 本题考查二次函数的最值问题、一次函数的有关知识,解题的关键是学会分类讨论,注意解题的严谨性,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
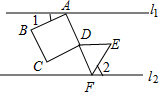 如图,直线l1∥l2,正方形ABCD的顶点A在l1上,顶点B、C、D在l1下方,等边三角形DEF的顶点F在上l2,顶点D、E在l2上方,且点A、D、F在同一直线上,若∠2=60°,则∠1的大小为( )
如图,直线l1∥l2,正方形ABCD的顶点A在l1上,顶点B、C、D在l1下方,等边三角形DEF的顶点F在上l2,顶点D、E在l2上方,且点A、D、F在同一直线上,若∠2=60°,则∠1的大小为( )| A. | 30° | B. | 60° | C. | 45° | D. | 15° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
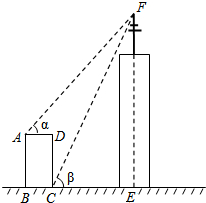 如图,某高楼顶部有一信号发射塔,小凡在矩形建筑物ABCD的A、C两点处测得塔顶F的仰角分别为α和β,AD=18m,CD=78m.
如图,某高楼顶部有一信号发射塔,小凡在矩形建筑物ABCD的A、C两点处测得塔顶F的仰角分别为α和β,AD=18m,CD=78m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是( )
如图,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是( )| A. | $\frac{4}{3}$π-$\sqrt{3}$ | B. | π | C. | π-$\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com