解下列一元二次方程:
(1)2x2-3x-5=0(公式法)
(2)3x2+2x-5=0(配方法)
(3)(2-3x)(x+4)=(3x-2)(1-5x);
解:(1)2x
2-3x-5=0
a=2,b=-3,c=-5
∴x=

=
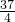
∴x
1=-1,
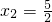
;
(2)3x
2+2x-5=0
3x
2+2x=5
x
2+

x=

(x+

)
2=

∴x+

=±

∴x
1=1,x
2=

;
(3)(2-3x)(x+4)=(3x-2)(1-5x)
(2-3x)(x+4)-(3x-2)(1-5x)=0
(2-3x)(5-4x)=0
∴x
1=

,x
2=

.
分析:(1)对于一元二次方程ax
2+bx+c=0(a≠0),若b
2-4ac≥0,一元二次方程的根为:x=

.
(2)首先移项把常数项移到等号右边,二次项系数化为1,然后方程左右两边同时加上一次项系数的一半的平方,即可配方;
(3)首先移项,把方程右边变成0,左边可以提公因式分解,因而可以用因式分解法求解.
点评:本题考查了解一元二次方程的方法,当把方程通过移项把等式的右边化为0后方程的左边能因式分解时,一般情况下是把左边的式子因式分解,再利用积为0的特点解出方程的根.因式分解法是解一元二次方程的一种简便方法,要会灵活运用.当化简后不能用分解因式的方法即可考虑求根公式法,此法适用于任何一元二次方程.

 =
=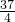
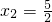 ;
; x=
x=
 )2=
)2=
 =±
=±
 ;
; ,x2=
,x2= .
. .
.
