

分析 (1)由点C的坐标以及tan∠OAC=$\frac{3}{4}$可得出点A的坐标,结合点A、C的坐标利用待定系数法即可求出抛物线的解析式;
(2)设直线AC的解析式为y=kx+b,由点A、C的解析式利用待定系数法即可求出直线AC的解析式,设N(x,0)(-4<x<0),可找出H、P的坐标,由此即可得出PH关于x的解析式,利用配方法即二次函数的性质即可解决最值问题;
(3)过点M作MK⊥y轴于点K,交对称轴于点G,根据角的计算依据正方形的性质即可得出△MCK≌△MEG(AAS),进而得出MG=CK.设出点M的坐标利用正方形的性质即可得出点G、K的坐标,由正方形的性质即可得出关于x的含绝对值符号的一元二次方程,解方程即可求出x值,将其代入抛物线解析式中即可求出点M的坐标.
解答 解:(1)∵C(0,3),
∴OC=3,
∵tan∠OAC=$\frac{3}{4}$,
∴OA=4,
∴A(-4,0).
把A(-4,0)、C(0,3)代入y=ax2+2ax+c中,
得$\left\{\begin{array}{l}{16a-8a+c=0}\\{c=3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=-\frac{3}{8}}\\{c=3}\end{array}\right.$,
∴抛物线的解析式为y=-$\frac{3}{8}$x2-$\frac{3}{4}$x+3.
(2)设直线AC的解析式为y=kx+b,
把A(-4,0)、C(0,3)代入y=kx+b中,
得:$\left\{\begin{array}{l}{-4k+b=0}\\{b=3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=3}\end{array}\right.$,
∴直线AC的解析式为y=$\frac{3}{4}$x+3.
设N(x,0)(-4<x<0),则H(x,$\frac{3}{4}$x+3),P(x,-$\frac{3}{8}$x2-$\frac{3}{4}$x+3),
∴PH=-$\frac{3}{8}$x2-$\frac{3}{4}$x+3-($\frac{3}{4}$x+3)=-$\frac{3}{8}$x2-$\frac{3}{2}$x=-$\frac{3}{8}$(x+2)2+$\frac{3}{2}$,
∵-$\frac{3}{8}$<0,
∴PH有最大值,
当x=-2时,PH取最大值,最大值为$\frac{3}{2}$.
(3)过点M作MK⊥y轴于点K,交对称轴于点G,则∠MGE=∠MKC=90°,
∴∠MEG+∠EMG=90°,
∵四边形CMEF是正方形,
∴EM=MC,∠MEC=90°,
∴∠EMG+∠CMK=90°,
∴∠MEG=∠CMK.
在△MCK和△MEG中,$\left\{\begin{array}{l}{∠MEG=∠CMK}\\{∠MGE=∠CKM=90°}\\{EM=MC}\end{array}\right.$,
∴△MCK≌△MEG(AAS),
∴MG=CK.
由抛物线的对称轴为x=-1,设M(x,-$\frac{3}{8}$x2-$\frac{3}{4}$x+3),则G(-1,-$\frac{3}{8}$x2-$\frac{3}{4}$x+3),K(0,-$\frac{3}{8}$x2-$\frac{3}{4}$x+3),
∴MG=|x+1|,CK=|-$\frac{3}{8}$x2-$\frac{3}{4}$x+3-3|=|-$\frac{3}{8}$x2-$\frac{3}{4}$x|=|$\frac{3}{8}$x2+$\frac{3}{4}$x|,
∴|x+1|=|$\frac{3}{8}$x2+$\frac{3}{4}$x|,
∴$\frac{3}{8}$x2+$\frac{3}{4}$x=±(x+1),
解得:x1=-4,x2=-$\frac{2}{3}$,x3=-$\frac{4}{3}$,x4=2,
代入抛物线解析式得:y1=0,y2=$\frac{10}{3}$,y3=$\frac{10}{3}$,y4=0,
∴点M的坐标是(-4,0),(-$\frac{2}{3}$,$\frac{10}{3}$),(-$\frac{4}{3}$,$\frac{10}{3}$)或(2,0).
点评 本题考查了待定系数法求函数解析式、二次函数的性质、正方形的性质以及全等三角形的判定与性质,解题的关键是:(1)利用待定系数法求出抛物线解析式;(2)根据二次函数的性质解决最值问题;(3)根据正方形的性质得出关于x的含绝对值符号的一元二次方程.本题属于中档题,难度不大,解决该题型题目时,根据正方形的性质找出关于x的含绝对值符号的一元二次方程,解方程求出点的横坐标是关键.


科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,菱形ABCD的对角线AC,BD相交于O,点E,F分别是AD,DC的中点.已知OE=$\frac{5}{2}$,EF=3,求菱形ABCD的周长和面积.
已知:如图,菱形ABCD的对角线AC,BD相交于O,点E,F分别是AD,DC的中点.已知OE=$\frac{5}{2}$,EF=3,求菱形ABCD的周长和面积.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
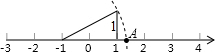 如图,数轴上的点A所表示的数为x,则x的值为( )
如图,数轴上的点A所表示的数为x,则x的值为( )| A. | $\sqrt{5}$ | B. | $\sqrt{5}$+1 | C. | $\sqrt{5}$-1 | D. | 1-$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 周长相等的锐角三角形都全等 | B. | 周长相等的直角三角形都全等 | ||
| C. | 周长相等的等腰直角三角形都全等 | D. | 周长相等的钝角三角形都全等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,为测量池塘边上两点A,B之间的距离,小明在池塘的一侧选取一点O,取OA,OB的中点D,E,测出DE=12米,那么A,B间的距离是( )
如图,为测量池塘边上两点A,B之间的距离,小明在池塘的一侧选取一点O,取OA,OB的中点D,E,测出DE=12米,那么A,B间的距离是( )| A. | 24米 | B. | 20米 | C. | 30米 | D. | 18米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com