
 如图,PA、PB分别切⊙O于A、B,点C、M是⊙O上的点,∠AMB=60°,过点
如图,PA、PB分别切⊙O于A、B,点C、M是⊙O上的点,∠AMB=60°,过点分析 由切线长定理知:PA=PB,CE=CF,由△PEF的外心在PE上,知该三角形是直角三角形,由∠M=60°,可计算出∠P的度数,利用特殊角间关系,表示出AE、PE、PF、FB,利用EF=AE+BF可得方程,求出AE的长.
解答 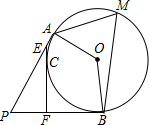 解:连接OA、OB.
解:连接OA、OB.
∵∠AMB=60°,
∴∠AOB=120°
∵PA、PB分别切⊙O于A、B,
∴PA=PB=3,∠OAP=∠OBP=90°,
在四边形PAOB中,∠P=360°-∠PAO-∠AOB-∠OBP=60°
∵△PEF的外心在PE上,
∴△PEF是直角三角形,且∠PFE=90°.
在Rt△PEF中,∵∠P=60°,
∴PE=2PF,EF=$\sqrt{3}$PF.
设AE的长为x,则PE=3-AE=3-x,
则PF=$\frac{1}{2}$(3-x),EF=$\frac{\sqrt{3}}{2}$(3-x),BF=3-PF=$\frac{1}{2}$(3+x)
∵EF是⊙O的切线,
∴EA=EC,FC=FB.
∵EF=EC+FC=AE+BF
∴$\frac{\sqrt{3}}{2}$(3-x)=x+$\frac{1}{2}$(3+x),
∴x=2$\sqrt{3}$-3.
点评 本题考查了外接圆、切线长定理、60°角所在直角三角形的边角关系、圆周角圆心角间关系及二次根式的相关计算,属于综合性较强的题目.表示出各个线段的长,并利用线段的和列出方程是解决本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | ①④ | B. | ①③④ | C. | ①③ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知△ABC的面积为a.延长△ABC的边BC到点D,延长边CA到点E,延长AB到点F,使CD=BC,AE=CA,BF=AB,连结DE,FD,FE.则阴影部分的面积为S=6a(用含a的代数式表示)
如图,已知△ABC的面积为a.延长△ABC的边BC到点D,延长边CA到点E,延长AB到点F,使CD=BC,AE=CA,BF=AB,连结DE,FD,FE.则阴影部分的面积为S=6a(用含a的代数式表示)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3x+1 | B. | -x-1 | C. | 6x2-3x+1 | D. | -2x2-x-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com