解:(1)原式=12x
2y•(-

x
2)-12x
2y•

xy+12x
2y•

y
2=-8x
4y-10x
3y
2+9x
2y
3;
(2)原式=4x
2-49-9x+6x
2-15+10x
=10x
2+x-64;
(3)原式=x
6+x
6-x
6=x
6;
(4)原式=1-4+

+

=-

;
(5)原式=16a
4÷(-4a
2)-8a
3÷(-4a
2)-4a
2÷(-4a
2)
=-4a
2+2a+1;
(6)解:原式=[(a-2b)-3c][(a-2b)+3c]
=(a-2b)
2-(3c)
2=a
2-4ab+4b
2-9c
2.
分析:(1)根据单项式乘以多项式法则计算即可;
(2)先根据平方差公式及多项式乘以多项式的法则展开,再合并同类项即可;
(3)根据幂的性质先算乘方,再算乘除法,最后合并同类项即可;
(4)先算乘方,再算加减即可;
(5)用多项式的每一项除以单项式,再把所得的结果相加减即可;
(6)根据平方差公式展开,再根据完全平方公式计算即可.
点评:本题主要考查对完全平方公式,平方差公式,同底数的幂的乘法、除法,多项式除以单项式,多项式乘多项式,幂的乘方与积的乘方等知识点的理解和掌握,能熟练地运用这些性质进行计算是解此题的关键.

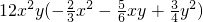
 x2)-12x2y•
x2)-12x2y• xy+12x2y•
xy+12x2y• y2
y2 +
+ =-
=- ;
;

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案